小屁孩的雙狹縫實驗

小明是個小屁孩喜歡打電動。問媽媽可不可以去打電動，媽媽有 0.4 的機率回答可以，有 0.6 的機率回答不可以。如果媽媽說可以，因為媽媽總是可以找到理由取消這個許可，例如，怎麼功課還沒寫、小提琴還沒拉、沒有把飯吃完，所以不是媽媽說可以就一定可以玩到爽；事實顯示這種情形小明有 0.6、0.3、0.1 的機率可以玩60分鐘、10分鐘、0分鐘。如果媽媽說不可以，因為媽媽可能在忙沒空理小明，所以不是媽媽說不可以就一定不能玩；事實顯示這種情形小明有 0.05、0.1、0.85 的機率可以玩60分鐘、10分鐘、0分鐘。所以如果沒有問媽媽，什麼是小明打電動的時間的機率分配？

畫成圖是：

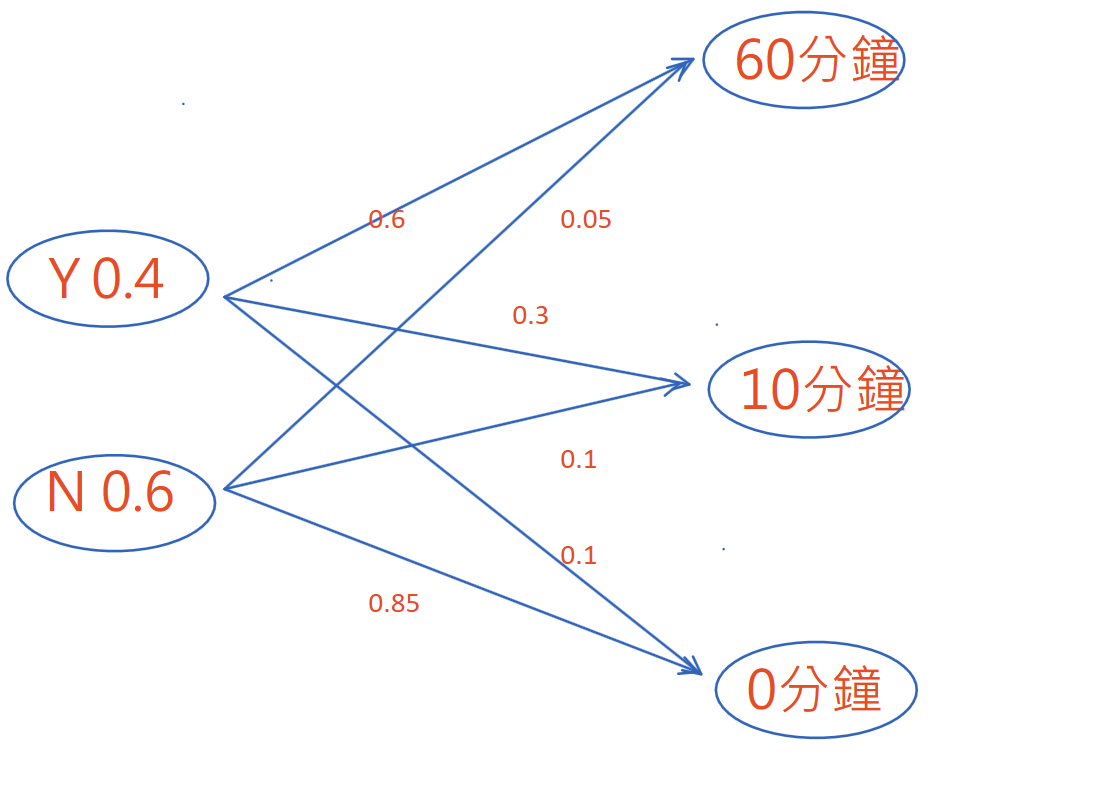
以Pr代表機率。因為就算沒有問媽媽，問媽媽也只有兩種可能性：可以或不可以，所以根據條件機率推理：

$\begin{aligned}\Pr(\text{play 60 mi}) &= \Pr(\text{mom ok}) \Pr(\text{play 60 mi} | \text{mom ok}) + \Pr(\text{mom not ok}) \Pr(\text{play 60 mi} | \text{mom not ok}) \\&= 0.4 \cdot 0.6+0.6 \cdot 0.05 =0.27\\\Pr(\text{play 10 mi}) &= \Pr(\text{mom ok}) \Pr(\text{play 10 mi} | \text{mom ok}) + \Pr(\text{mom not ok}) \Pr(\text{play 10 mi} | \text{mom not ok}) \\&= 0.4 \cdot 0.3+0.6 \cdot 0.1 =0.18\\\Pr(\text{play 0 mi}) &= \Pr(\text{mom ok}) \Pr(\text{play 0 mi} | \text{mom ok}) + \Pr(\text{mom not ok}) \Pr(\text{play 0 mi} | \text{mom not ok}) \\&= 0.4 \cdot 0.1+0.6 \cdot 0.85 =0.55\end{aligned}$

但是小明寧願不去問媽媽，因為長時間下來的實驗事實結果卻是，如果沒有問媽媽，則小明有0.40、0.33、0.27的機率玩60分鐘、10分鐘、0分鐘，和上述機率不同而且比較好。這該如何解釋呢？

量子雙狹縫實驗

量子雙狹縫實驗的圖示如下：

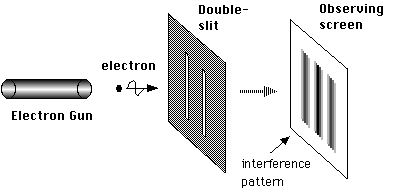
實驗大意是，銀幕上看到的落點累積的圖很怪，不是預料中的機率的分配圖。如果在左邊狹縫旁邊多裝個偵測器或是把其中一個狹縫遮起來，則在銀幕上看到的落點累積的圖就又回到古典機率的分配圖。如果認為原因是通過雙狹縫的東西是波，所以把偵測器放在狹縫和銀幕之間，先不要打開偵測器，等東西通過狹縫後但到達偵測器之前再打開偵測器去偵測，則銀幕上的圖卻又是古典機率的圖。原先的實驗的東西是光子，但多年下來實驗技術進步已經確認電子、原子核、或某些大分子也會有這個現象；如果房間有兩個門而我們能說"張三離開房間"卻不能說＂張三要不是走左邊的門離開就是走右邊的門離開＂，那很多習以為常的日常生活思維就不能用了；許多人以為量子現象是小尺度東西的專利，在日常生活中不用擔心，但是大尺度的量子現象也不是不可能，例如兩個人藉由一些實驗室設備就可以不溝通就打敗Bell inequality（請看這個遊戲 ），或許小明或其他人文科學碰到的類似的故事追根究底就是一個大尺度量子現象。

古典機率的解釋

測量有時候會改變被測量的東西，在小明這個問題裡，"問媽媽"這個動作就是一種測量。所以"不知道媽媽答案"和"媽媽回答是Y或者媽媽回答是N"是不一樣的事。所以圖解應該畫成：

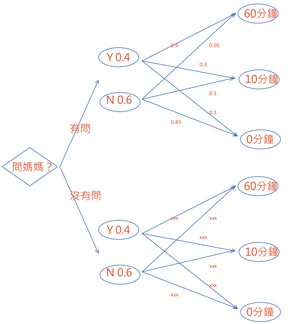
適當安排一下xxx的數字，就可以讓沒問媽媽的情況下有0.40、0.33、0.27的機率玩60分鐘、10分鐘、0分鐘了。

量子機率的解釋

既然需要兩倍的資訊量去描述，有科學家就想說那就用複數來描述這些可能性；複數有一個實部一個虛部，也有兩倍的資訊量，或許就不需要畫那麼大張圖了。十九世紀古典電子工程的發展讓這些科學家覺得虛數一點也不虛，在對複數頗有好感的情況下就這麼幹了，圖示如下：

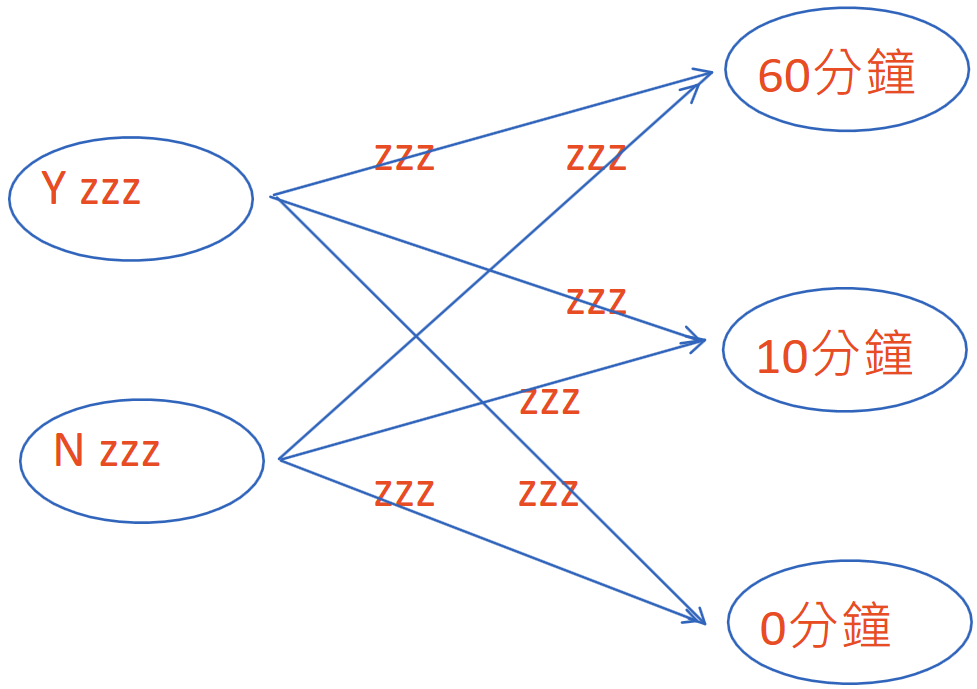
其中zzz是一些複數，稱之為量子機率。

假想圖的左邊有 $m$ 種狀態分別叫作 ，以 $L_1 ,  L_2 ,  \cdots L_a_1 , a_2 , \cdots a_m$ 表示這些狀態的量子機率，圖的右邊有 $n$ 種狀態分別叫作 $R_1 , R_2 ,\cdots R_n$ ，以 $b_1 , b_2 ,\cdots b_n$ 表示這些狀態的量子機率，圖的中間這些箭頭， $1 \leq i \leq m$ ， $1 \leq j \leq n$ ，從狀態 $L_i$ 到 $R_j$ 的量子機率是 $x_{i j}$ 。但是古典機率是正實數，那這些複數怎麼對應出這些古典機率呢？複數乘上自己的共軛複數也是正的，以 $A$ 和 $B$ 和 $X$ 表示古典機率，所以量子機率是這樣設計的：

$\begin{aligned}A_i &\equiv \Pr(L_i) = a_i \overline{a_i}\\B_j &\equiv \Pr(R_j) = b_j \overline{b_j}\\X_{i j} &\equiv \Pr(L_i \rightarrow R_j) = x_{i j} \overline{x_{i j}}\\b_j &= \sum_i a_i x_{i j}\end{aligned}$

問題一

量子機率要滿足哪些條件？

Ans: 因為古典機率全部加起來是1，所以量子機率需要滿足：

$1 = \sum_i a_i \overline{a_i} = \sum_j b_j \overline{b_j} = \sum_j x_{i j} \overline{x_{i j}}$                              ( 1 )

而且因為

$\begin{aligned}\sum_j b_j \overline{b_j} &= \sum_j {\sum_i a_i x_{i j} \sum_k \overline{a_k} \overline{x_{k j}}} \\&= \sum_{i,k} a_i \overline{a_k} \sum_j x_{i j} \overline{x_{k j}} \\&= \sum_i a_i \overline{a_i} \sum_j x_{i j} \overline{x_{i j}} + \sum_{i< k} a_i \overline{a_k} \sum_j x_{i j} \overline{x_{k j}} + a_k \overline{a_i} \sum_j x_{k j} \overline{x_{i j}}\\&= 1 + \sum_{i<k} a_i \overline{a_k} \sum_j x_{i j} \overline{x_{k j}} + a_k \overline{a_i} \sum_j x_{k j} \overline{x_{i j}}\\&= 1 + \sum_j \sum_{i< k} a_i \overline{a_k} x_{i j} \overline{x_{k j}} + a_k \overline{a_i} x_{k j} \overline{x_{i j}}\end{aligned}$

所以 $x_{i j}$ 必須滿足這個最弱的條件：

$0 = \sum_j \sum_{i< k} a_i \overline{a_k} x_{i j} \overline{x_{k j}} + a_k \overline{a_i} x_{k j} \overline{x_{i j}}$                 ( 2 )

或者 $x_{i j}$ 如果可以滿足這個較強的條件也ok：

當 $i \ne k$ 時候， $0 = \sum_j x_{i j} \overline{x_{k j}}$                                           ( 3 )

該怎麼找 $x_{i j}$ 呢？首先數一下未知數和條件的個數，未知數有 $4m n$ 個，如果用條件 (1) 和 (2) ，則條件共有 $m+1$ 個，因此 $4 m n \geq m + 1$ 的時候才有解，但是這個不等式一定會成立，所以一定可以找到滿足 (1) 和 (2) 的 $x_{i j}$ 。如果用條件 (1) 和 (3) ，則條件共有 $m + \frac{m ( m - 1 )}{2}$ 個，因此 $4 m n \geq m + \frac{m ( m - 1 )}{2}$ 的時候才有解，也就就是 $n \geq \frac{m + 1}{8}$ 時候才能找到滿足 (3) 的解。如果 $n< \frac{m + 1}{8}$ 則只能訴諸 (2) 去找這些量子機率。科學家常研究的是狀態隨著時間的變化，也就是$m=n$ 的情形，這時候這個不等式一定成立，所以這時候一定可以在 (3) 這個較強的條件下找到對應的量子機率。此時的狀態變換矩陣是個方陣，而 (1) 和 (3) 條件就是 Unitary 矩陣條件。

問題二

沒有任何額外條件，$L$ 有 $m$ 個狀態，$R$ 有 $m$ 個狀態，寫個程式隨便找一個符合 (1) 和 (3) 的量子機率 $x_{i j}$ ？並且造一個 $m=3$ 的例子和對應的矩陣。

Ans： 演算法大致是這樣。定義

$\begin{aligned}x_i &\equiv ( x_{i 1},x_{i 2},\cdots x_{i m} )\\x_i \overline{x_j} &\equiv \sum_k x_{i k} \overline{x_{j k}}\\ \begin{vmatrix}x_i\end{vmatrix} &\equiv \sqrt{x_i \overline{x_i}}\end{aligned}$

依照這個直交化基底的標準動作：

1. 隨機產生 $m^2$ 個複數擺進 $x_1,x_2,\cdots x_m$
2. 以 $\frac{1}{|x_1|} x_1$ 取代 $x_1$
3. $i$ 依序從 2 跑到 $m$，以 $x_i - \sum_{j < i} (x_i \overline{x_j}) x_j$ 取代 $x_i$ ，再以 $\frac{1}{|x_i|} x_i$ 取代 $x_i$

如此產生的 $x_1,x_2,\cdots x_ m$ 自然會滿足 (1) 和 (3)

$m=n=3$ 的例子，隨便給 9 個複數：

$\begin{aligned}x_1 &= (-0.226040207520038 - 0.357587726435739 i,0.722975401964589 - 0.0852203091010315 i ,0.270218885057131 + 0.0477353441449391 i)\\x_2 &= ( 0.0738076302569551 + 0.0488882283298338 i,-0.292836531099144 - 0.101264759881712 i,0.672010719751796 + 0.497111427369494 i)\\x_3 &= (0.391467101019704 + 0.187645169982295 i, 0.0769290714780256 - 0.264441497979309 i,- 0.159954254250136 + 0.810990749245041 i)\end{aligned}$

根據這個演算法就產生：

$\begin{aligned}x_1 &= (- 0.255251232701256 - 0.403798549704793 i , 0.816405030719095 - 0.0962332727786583 i,0.305139091256043 + 0.0539041508150016 i)\\x_2 &= ( 0.0622967150588796 + 0.0446190056105974 i,- 0.296705780793108 - 0.137051233446262 i , 0.76457952368663 + 0.550208192091991 i )\\x_3 &=(0.81417198095865 + 0.321007458657672 i,0.356788890322766 - 0.300177130747684 i ,0.0751455736378119 - 0.105008178676672 i)\end{aligned}$

排成矩陣是：

$\begin{aligned}x_{i j}&=(L_i \rightarrow R_j)\\x &= \begin{bmatrix}- 0.255251232701256 - 0.403798549704793 i& 0.816405030719095 - 0.0962332727786583 i &0.305139091256043 + 0.0539041508150016 i\\ 0.0622967150588796 + 0.0446190056105974 i& - 0.296705780793108 - 0.137051233446262 i&0.76457952368663 + 0.550208192091991 i\\ 0.81417198095865 + 0.321007458657672 i& 0.356788890322766 - 0.300177130747684 i& 0.0751455736378119 - 0.105008178676672 i\end{bmatrix}\end{aligned}$

問題三

隨便找出一個滿足小明有問媽媽時候的A和X的古典機率的量子機率，並計算這個時候量子機率所對應的有"問媽媽"這個測量動作和沒"問媽媽"這個測量動作的兩種情況下玩電動的時間的古典機率分配。

Ans: 以 $\theta_{a_i}$ 表示 $a_i$ 這個複數的角度，以 $\theta_{x_{i j}}$ 表示 $x_{i j}$ 這個複數的角度，利用 Excel 裡面關於複數的函數（IM開頭的一些函數）玩一玩規劃求解，確認 $x_{i j}$ 符合 (1) 和 (3) 條件：

$\begin{aligned}a_1 &= \sqrt{0.4} \exp(\theta_{a_1} i),a_2 = \sqrt{0.6} \exp(\theta_{a_2} i),\theta_{a_1} = \theta_{a_2} = 0.523598776\\x_{11} &= \sqrt{0.6} \exp(\theta_{x_{11}} i),x_{12} = \sqrt{0.3} \exp(\theta_{x_{12}} i), x_{13} = \sqrt{0.1} \exp(\theta_{x_{13}} i),\theta_{x_{11}} = 0.295847422 ,\theta_{x_{12}} = 1.636677659 ,\theta_{x_{13}} = 0.012675129\\x_{21} &= \sqrt{0.05} \exp(\theta_{x_{21}} i) ,x_{22} = \sqrt{0.1} \exp(\theta_{x_{22}} i) ,x_{23} = \sqrt{0.85} \exp(\theta_{x_{23}} i),\theta_{x_{21}} = 0.001020734 ,\theta_{x_{22}} = 0.200836122 ,\theta_{x_{23}} = 2.288933412\end{aligned}$ 有"問媽媽"這個測量動作的情形。沒有任何量子機率需要加起來。所以只差計算複數乘上自己的共軛得到古典機率和用一次古典機率的貝氏定理去得到答案：

$\begin{aligned}B_1 &= A_1 X_{11} + A_2 X_{21} = a_1 \overline{a_1} x_{11} \overline{x_{11}} + a_2 \overline{a_2} x_{21} \overline{x_{21}} = 0.4 \cdot 0.6 + 0.6 \cdot 0.05 = 0.27\\B_2 &= A_1 X_{12} + A_2 X_{22} = a_1 \overline{a_1} x_{12} \overline{x_{12}} + a_2 \overline{a_2} x_{22} \overline{x_{22}} = 0.4 \cdot 0.3 + 0.6 \cdot 0.1 = 0.18\\B_3&= A_1 X_{13} + A_2 X_{23} = a_1 \overline{a_1} x_{13} \overline{x_{13}} + a_2 \overline{a_2} x_{23} \overline{x_{23}} = 0.4 \cdot 0.1 + 0.6 \cdot 0.85 = 0.55\end{aligned}$

沒有"問媽媽"這個測量動作的情形。不能確定路徑的時候，要先計算量子機率，所以：

$\begin{aligned}b_1 &= \sum_i a_i x_{i1} = 0.484328607027089 + 0.444757301420366 i\\b_2 &= \sum_i a_i x_{i2} = - 0.00914350829514099 + 0.450277166762998 i\\b_3 &= \sum_i a_i x_{i3} = - 0.503902802388064 + 0.33296545453821 i\\B_1 &= b_1 \overline{b_1} = 0.432383257\\B_2 &= b_2 \overline{b_2} = 0.202833131\\B_3 &= b_3 \overline{b_3} = 0.364784028\end{aligned}$

問題四

什麼條件才能中間沒測量時候讓量子機率的結論和對應的古典機率結論一樣？

Ans: 用古典和量子的說法分別計算出現在狀態 $R_j$ 的機率，古典方法是 $\sum_i A_i X_{i j}$ ，量子方法是 $b_j \overline{b_j}$ 其中 $b_j = \sum_i a_i x_{i j}$ 。所以如果這兩個數字要相等，就是：

$\sum_i a_i \overline{a_i} x_{i j} \overline{x_{i j}} = \sum_i a_i x_{i j} \sum_k \overline{a_k x_{k j}} = \sum_{i,k} a_i \overline{a_k} x_{i j} \overline{x_{k j}}= \sum_i a_i \overline{a_i} x_{i j} \overline{x_{i j}} + \sum_{i<k} a_i \overline{a_k} x_{i j} \overline{x_{k j}} + a_k \overline{a_i} x_{k j} \overline{x_{i j}}$

也就是對於所有 $j$

$0 = \sum_{i<k} a_i \overline{a_k} x_{i j} \overline{x_{k j}} + a_k \overline{a_i} x_{k j} \overline{x_{i j}}$                                      ( 4 )

這個條件剛好也導致 (2) 成立，所以一定有辦法把古典機率的問題放進量子機率的架構，但是反過來卻未必，問題三就是個例子。給定一個古典機率的 $A_i$ 和 $X_{i j}$ ，如何去找符合這個條件的 $a_i$ 和 $x_{i j}$ 呢？先確定一下可行性， $a_i$ 和 $x_{i j}$ 只剩下角度還沒確認，所以總共有$m+m n$ 個未知數，需要滿足的條件只有 (4)，所以 $m + m n \geq n$ 才有解，這不等式一定成立，甚至還有$m+m n-n$ 個自由度可以玩，例如當 $m=2$ 的時候，可以選擇所有的 $a_i$ 都是一樣的角度， $x_{1j}$ 和 $x_{2j}$ 相差 90 度角，或是選擇所有的 $x_{i j}$ 都是實數， $a_1$ 和 $a_2$ 相差 90 度角：

$\sum_{i<k} a_i \overline{a_k} x_{i j} \overline{x_{k j}} + a_k \overline{a_i} x_{k j} \overline{x_{i j}} = \sqrt{A_1} \sqrt{A_2} \sqrt{X_{1j}} \sqrt{X_{2j}} i - \sqrt{A_2} \sqrt{A_1} \sqrt{X_{2j}} \sqrt{X_{1j}} i = 0$

問題五

如果沒有問媽媽的時候的玩電動時間的機率分配真的如古典機率所預測，隨便找出一組小明雙狹縫實驗的量子機率，並且驗算一下。

Ans: 根據問題四的答案，可以選擇：

$\begin{aligned}a_1 &= \sqrt{0.4} \exp(\theta_{a_1} i),a_2 = \sqrt{0.6} \exp(\theta_{a_2} i),\theta_{a_1} = \theta_{a_2} = 0.523598776\\x_{11} &= \sqrt{0.6} \exp(\theta_{x_{11}} i),x_{12} = \sqrt{0.3} \exp(\theta_{x_{12}} i),x_{13} = \sqrt{0.1} \exp(\theta_{x_{13}} i),\theta_{x_{1j}} = \frac{\pi}{4}\\x_{21} &= \sqrt{0.05} \exp(\theta_{x_{21}} i),x_{22} = \sqrt{0.1} \exp(\theta_{x_{22}} i),x_{23} = \sqrt{0.85} \exp(\theta_{x_{23}} i),\theta_{x_{2j}} = \frac{-\pi}{4}\end{aligned}$

所以

$\begin{aligned}b_1 &= \sum_i a_i x_{i1} = 0.294098179990674 + 0.428376307148485 i\\b_2 &= \sum_i a_i x_{i2} = 0.326260087595249 + 0.271209061873567 i\\b_3 &= \sum_i a_i x_{i3} = 0.741572824592954 + 0.00835139660346801 i\\B_1 &= b_1 \overline{b_1} = 0.27\\B_2 &= b_2 \overline{b_2} = 0.18\\B_3 &= b_3 \overline{b_3} = 0.55\end{aligned}$

問題六

隨便找出一組符合小明雙狹縫實驗事實的量子機率。

Ans: 數一下未知數和條件的個數。未知數總共有 $m n+m+n$ 個。條件的部分，如果打算滿足 (2) 則有 1 個，所以永遠成立，如果打算滿足 (3) 則條件有 $\frac{m(m-1)}{2}$個，所以 $n$ 不能太小，必須 $m n + m + n \geq \frac{m ( m - 1 )}{2}$ ，也就是 $n \geq \frac{m ( m - 3 )}{2 ( m + 1 )}$ ，小明的問題是 $m=2, n=3$，所以這兩種找法都可以試試去找解。這裡用 (3) 找：

$\begin{aligned}a_1 &= \sqrt{0.4} \exp(i),a_2 = \sqrt{0.6} \exp(-i)\\x_{11} &= \sqrt{0.6} \exp(\theta_{x_{11}} i),x_{12} = \sqrt{0.3} \exp(\theta_{x_{12}} i),x_{13} = \sqrt{0.1} \exp(\theta_{x_{13}} i)\\x_{21} &= \sqrt{0.05} \exp(\theta_{x_{21}} i),x_{22} = \sqrt{0.1} \exp(\theta_{x_{22}} i),x_{23} = \sqrt{0.85} \exp(\theta_{x_{23}} i)\\B_1 &= 0.40,B_2 = 0.33,B_3 =0.27\end{aligned}$

藉由 Excel 規劃求解去找得到：

$\begin{aligned}\theta_{x_{11}} &= 4.93676250343613,\theta_{x_{12}} = 3.02973882509439,\theta_{x_{13}} = 2.53856194461586\\\theta_{x_{21}} &= 6.23861330546238,\theta_{x_{22}} = 5.4726170722089,\theta_{x_{23}} =1.26933359601616\end{aligned}$

所以

$\begin{aligned}b_1 &= \sum_i a_i x_{i1} = 0.547790808181799 - 0.316109751002095 i\\b_2 &= \sum_i a_i x_{i2} = - 0.276704114208954 - 0.5067224033457 i\\b_3 &= \sum_i a_i x_{i3} = 0.503949479320372 + 0.112700620220305 i\\B_1 &= b_1 \overline{b_1} = 0.400000144\\B_2 &= b_2 \overline{b_2} = 0.333332761\\B_3 &= b_3 \overline{b_3} = 0.266666508\end{aligned}$

只要一做測量，原本藉由量子機率無以名狀地散在各個量子狀態的東西就會變成一個出現在某個唯一狀態的東西。測量是一種干擾，一般而言越大的系統因為受到越多的干擾就好像無時無刻被測量，所以越大的系統越像古典機率描述的系統。一個天文數字粒子構成的人體要能穿牆的機率可能需要100億年才能看到一次。

問題七

某個系統有三個狀態用問題二的矩陣來描述每天的變化，一開始的狀態是 $L_1$ ，計算下面三種實驗計畫的五天後測量出現在各狀態的機率。1，每天都有測量。2，第二天後有測量。3，每天都沒有測量。

Ans：

$x = \begin{bmatrix}- 0.255251232701256 - 0.403798549704793 i& 0.816405030719095 - 0.0962332727786583 i &0.305139091256043 + 0.0539041508150016 i\\ 0.0622967150588796 + 0.0446190056105974 i& - 0.296705780793108 - 0.137051233446262 i& 0.76457952368663 + 0.550208192091991 i\\ 0.81417198095865 + 0.321007458657672 i& 0.356788890322766 - 0.300177130747684 i& 0.0751455736378119 - 0.105008178676672 i\end{bmatrix}$

如果某一天有測量所以確定了狀態，例如是 $L_1$ ，對應的量子機率分配是 $a = (\exp(\theta i),0,0)$ 。隔天的量子機率分配是 $a x = ( \exp( \theta i ) x_{11},\exp( \theta i ) x_{12},\exp( \theta i ) x_{13} )$ 。所以如果隔天有測量，則出現在各個狀態的古典機率是 $( x_{11} \overline{x_{11}}, x_{12} \overline{x_{12}} , x_{13} \overline{x_{13}} )$ ，所以如果測量第某天的狀態然後統計下來有古典機率分配 $A$ 而且隔天也有測量的話，則隔天看到的古典機率分配是 $A X$ ，其中 $X_{i j} = x_{i j} \overline{x_{i j}}$ 。在這個例子裏 $X$ 是：

$X = \begin{bmatrix}0.228206461& 0.675778017& 0.096015522\\ 0.005871736& 0.106817361& 0.887310903\\ 0.765921803& 0.217404622& 0.016673575\end{bmatrix}$

一開始的古典機率分配是 $A = (1,0,0)$ ，以下分別解這三種實驗計畫的情形，要做矩陣的計算可以到 http://comnuan.com ，google查詢也可以做簡單的複數計算（http://comnuan.com 和google 查詢虛數符號是 i ）。

===== 每天都有測量 =====

機率分配是

$\begin{aligned}&A X X X X X = A X^5 \\&= \begin{bmatrix}1& 0& 0\end{bmatrix} \begin{bmatrix}0.281637907& 0.309534982& 0.40882711\\ 0.424265447& 0.302427424& 0.27330712\\ 0.294096646& 0.388037594& 0.31786576\end{bmatrix} \\&= \begin{bmatrix}0.281637907& 0.309534982& 0.40882711\end{bmatrix}\end{aligned}$ 所以雖然每次實驗都只會出現一個特定狀態，但是長期實驗下來會有 0.281637907 的機率出現在 $L_1$ ，0.309534982 的機率出現在 $L_2$ ，0.40882711的機率出現在 $L_3$ 。

===== 第二天和第五天有測量 =====

第二天後的量子機率分配是

$\begin{aligned}&a x x = a x^2 \\&= \begin{bmatrix}\exp(\theta i)&0&0\end{bmatrix} \begin{bmatrix}0.188385171492828 + 0.378411492495113 i& - 0.377617196181361 - 0.460799228725275 i& 0.649624422042887 + 0.210649480770776 i\\ 0.435625362638781 + 0.635078885623020 i& 0.562357860511993 + 0.078558832983676 i& - 0.019613312718044 - 0.290004856694682 i\\ 0.052314154521726 - 0.474851925559519 i& 0.543874779206007 + 0.163864868042358 i& 0.663705599815701 + 0.092856256479830 i\end{bmatrix} \\&= \exp(\theta i) \begin{bmatrix}0.188385171492828 + 0.378411492495113 i& - 0.377617196181361 - 0.460799228725275 i& 0.649624422042887 + 0.210649480770776 i\end{bmatrix}\end{aligned}$

因為有測量，所以第二天後會看到一個古典機率分配是： $(0.17868423049, 0.35493067604, 0.46638509346)$ 。

如果這時候是出現在，比方說， $L_1$ ，則接下來三天後的量子機率分配是

$\begin{aligned}&\begin{bmatrix}\exp(\theta i)&0&0\end{bmatrix} x x x = \begin{bmatrix}\exp(\theta i)&0&0\end{bmatrix} x^3\\&= \begin{bmatrix}\exp(\theta i)&0&0\end{bmatrix} \begin{bmatrix}0.563038505198970 + 0.161824348840283 i& 0.534113413864006 + 0.359437821432993 i& 0.072839182594411 - 0.486849349305052 i\\ 0.253902964918139 - 0.550433600633106 i& 0.166623576207690 + 0.278596201401855 i& 0.453509795472489 + 0.567014763058754 i\\ 0.332035305448733 + 0.423212964618469 i& 0.122776184414566 - 0.681963388028161 i& 0.426860514614723 + 0.219739367221732 i\end{bmatrix}\\&= \exp(\theta i) \begin{bmatrix}0.563038505198970 + 0.161824348840283 i& 0.534113413864006 + 0.359437821432993 i& 0.072839182594411 - 0.486849349305052 i\end{bmatrix}\end{aligned}$

因為會有第五天的測量，所以三天後會看到一個古典機率分配是： $(0.34319947821, 0.41447268634, 0.24232783544)$ 。如果第二天後是出現在 $L_2$ 或 $L_3$ 類似的推理也一樣，所以第五天後會看到的古典機率分配是：

$\begin{aligned}&\begin{bmatrix}0.17868423049& 0.35493067604& 0.46638509346\end{bmatrix} \begin{bmatrix}0.34319947821& 0.41447268634& 0.24232783544\\ 0.3674438643& 0.10537925958& 0.52717687611\\ 0.28935665748& 0.48014805407& 0.23049528844\end{bmatrix}\\&= \begin{bmatrix}0.326693065573355& 0.335395959933184& 0.337910974473460\end{bmatrix}\end{aligned}$

所以雖然每次實驗都只會出現一個特定狀態，但是長期實驗下來會有 0.326693065573355 的機率出現在 $L_1$ ， 0.335395959933184 的機率出現在 $L_2$ ， 0.337910974473460 的機率出現在 $L_3$ 。

===== 只有第五天有測量 =====

第五天後的量子機率分配是

$\begin{aligned}&a x x x x x = a x^5\\&= \begin{bmatrix}\exp( \theta i )& 0& 0\end{bmatrix} \begin{bmatrix}- 0.178136940210836 + 0.679272993573969 i& 0.253474273100002 - 0.329312654414754 i& 0.518989110370822 - 0.254577498158470 i\\ 0.444749878184810 + 0.033881856305437 i& - 0.123962878425866 + 0.643314771867446 i& 0.606762452728871 + 0.060565672586457 i\\ 0.515661355304950 - 0.204935021522311 i&0.388403472620588 - 0.497218282089973 i& 0.189273448680794 + 0.508121331607858 i\end{bmatrix}\\&= \exp(\theta i) \begin{bmatrix}- 0.178136940210836 + 0.679272993573969 i& 0.253474273100002 - 0.329312654414754 i& 0.518989110370822 - 0.254577498158470 i\end{bmatrix}\end{aligned}$

所以雖然每次實驗都只會出現一個特定狀態，但是長期實驗下來會有 0.49314456926 的機率出現在 $L_1$ ，0.17269603148 的機率出現在 $L_2$ ，0.33415939925 的機率出現在 $L_3$ 。