QuantumMeasurement

HomePage | Memberswill go by tor | RecentChanges | Join |

measure operation is generally not commutative with unitary operation but sometimes possible. Consider this nn qbits unitary KK with the row and column index integer using binary representation:

[K(000⟩) K(001⟩) K(010⟩) K(011⟩) K(100⟩) K(101⟩) K(110⟩) K(111⟩)] =[000⟩ 001⟩ 010⟩ 011⟩ 100⟩ 101⟩ 110⟩ 111⟩]⋅ [K 000,000 K 000,001 K 000,010 K 000,011 K 000,100 K 000,101 K 000,110 K 000,111 K 001,000 K 001,001 K 001,010 K 001,011 K 001,100 K 001,101 K 001,110 K 001,111 K 010,000 K 010,001 K 010,010 K 010,011 K 010,100 K 010,101 K 010,110 K 010,111 K 011,000 K 011,001 K 011,010 K 011,011 K 011,100 K 011,101 K 011,110 K 011,111 K 100,000 K 100,001 K 100,010 K 100,011 K 100,100 K 100,101 K 100,110 K 100,111 K 101,000 K 101,001 K 101,010 K 101,011 K 101,100 K 101,101 K 101,110 K 101,111 K 110,000 K 110,001 K 110,010 K 110,011 K 110,100 K 110,101 K 110,110 K 110,111 K 111,000 K 111,001 K 111,010 K 111,011 K 111,100 K 111,101 K 111,110 K 111,111]\begin{aligned}&\begin{bmatrix}K({000}\rangle)&K({001}\rangle)&K({010}\rangle)&K({011}\rangle)&K({100}\rangle)&K({101}\rangle)&K({110}\rangle)&K({111}\rangle)\end{bmatrix}\\&=\begin{bmatrix}{000}\rangle&{001}\rangle&{010}\rangle&{011}\rangle&{100}\rangle&{101}\rangle&{110}\rangle&{111}\rangle\end{bmatrix} \cdot \\& \begin{bmatrix}K_{000,000}&K_{000,001}&K_{000,010}&K_{000,011}&K_{000,100}&K_{000,101}&K_{000,110}&K_{000,111}\\K_{001,000}&K_{001,001}&K_{001,010}&K_{001,011}&K_{001,100}&K_{001,101}&K_{001,110}&K_{001,111}\\K_{010,000}&K_{010,001}&K_{010,010}&K_{010,011}&K_{010,100}&K_{010,101}&K_{010,110}&K_{010,111}\\K_{011,000}&K_{011,001}&K_{011,010}&K_{011,011}&K_{011,100}&K_{011,101}&K_{011,110}&K_{011,111}\\K_{100,000}&K_{100,001}&K_{100,010}&K_{100,011}&K_{100,100}&K_{100,101}&K_{100,110}&K_{100,111}\\K_{101,000}&K_{101,001}&K_{101,010}&K_{101,011}&K_{101,100}&K_{101,101}&K_{101,110}&K_{101,111}\\K_{110,000}&K_{110,001}&K_{110,010}&K_{110,011}&K_{110,100}&K_{110,101}&K_{110,110}&K_{110,111}\\K_{111,000}&K_{111,001}&K_{111,010}&K_{111,011}&K_{111,100}&K_{111,101}&K_{111,110}&K_{111,111}\end{bmatrix}\end{aligned}

To highlight the probability of the 1st qbit, denote the input quantum state by

∑ x∈{0,1} n−1a x0x⟩+b x1x⟩\sum_{x \in \{0,1\}^{n-1}} a_x {0x}\rangle + b_x {1x}\rangle

Case 1 Measure all qbits at the final

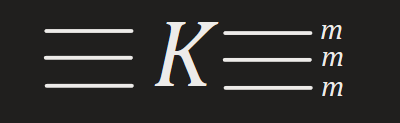
After the KK, the quantum state is

K(∑ x∈{0,1} n−1a x0x⟩+b x1x⟩)=∑ x∈{0,1} n−1a xK(0x⟩)+b xK(1x⟩)K \left(\sum_{x \in \{0,1\}^{n-1}} a_x {0x}\rangle + b_x {1x}\rangle \right) = \sum_{x \in \{0,1\}^{n-1}} a_x K({0x}\rangle) + b_x K({1x}\rangle)

As

K(0x⟩) =∑ y∈{0,1} ny⟩K y,0x=∑ y∈{0,1} n−10y⟩K 0y,0x+1y⟩K 1y,0x K(1x⟩) =∑ y∈{0,1} n−10y⟩K 0y,1x+1y⟩K 1y,1x\begin{aligned}K({0x}\rangle) &= \sum_{y \in \{0,1\}^n} {y}\rangle K_{y,0x} = \sum_{y \in \{0,1\}^{n-1}} {0y}\rangle K_{0y,0x} + {1y}\rangle K_{1y,0x}\\K({1x}\rangle) &= \sum_{y \in \{0,1\}^{n-1}} {0y}\rangle K_{0y,1x} + {1y}\rangle K_{1y,1x}\end{aligned}

The final quantum state is

∑ x∈{0,1} n−1a x(∑ y∈{0,1} n−10y⟩K 0y,0x+1y⟩K 1y,0x)+b x(∑ y∈{0,1} n−10y⟩K 0y,1x+1y⟩K 1y,1x) =∑ y∈{0,1} n−10y⟩(∑ x∈{0,1} n−1a xK 0y,0x+b xK 0y,1x)+1y⟩(∑ x∈{0,1} n−1a xK 1y,0x+b xK 1y,1x)\begin{aligned}&\sum_{x \in \{0,1\}^{n-1}} a_x \left(\sum_{y \in \{0,1\}^{n-1}} {0y}\rangle K_{0y,0x} + {1y}\rangle K_{1y,0x} \right) + b_x \left( \sum_{y \in \{0,1\}^{n-1}} {0y}\rangle K_{0y,1x} + {1y}\rangle K_{1y,1x} \right)\\&= \sum_{y \in \{0,1\}^{n-1}} {0y}\rangle \left( \sum_{x \in \{0,1\}^{n-1}} a_x K_{0y,0x} + b_x K_{0y,1x} \right) + {1y}\rangle \left( \sum_{x \in \{0,1\}^{n-1}} a_x K_{1y,0x} + b_x K_{1y,1x}\right)\end{aligned}

So, the probability at 0y⟩{0y}\rangle state is

∣∑ x∈{0,1} n−1a xK 0y,0x+b xK 0y,1x∣ 2\begin{vmatrix}\sum_{x \in \{0,1\}^{n-1}} a_x K_{0y,0x} + b_x K_{0y,1x}\end{vmatrix}^2

Case 2 Measure 1st qbit before apply KK

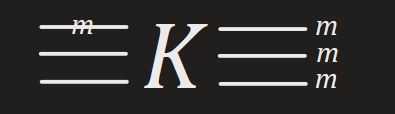
Let

s 0≡∑ x∈{0,1} n−1∣a x∣ 2 s 1≡∑ x∈{0,1} n−1∣b x∣ 2\begin{aligned}s_0 \equiv \sqrt{\sum_{x \in \{0,1\}^{n-1}} \begin{vmatrix}a_x\end{vmatrix}^2}\\s_1 \equiv \sqrt{\sum_{x \in \{0,1\}^{n-1}} \begin{vmatrix}b_x\end{vmatrix}^2}\end{aligned}

The input state to KK becomes two quantum states with probability s 0 2s_0^2 or s 1 2s_1^2 :

∑ x∈{0,1} n−1a xs 00x⟩\sum_{x \in \{0,1\}^{n - 1}} \frac{a_x}{s_0} {0x}\rangle

or

∑ x∈{0,1} n−1b xs 11x⟩\sum_{x \in \{0,1\}^{n - 1}} \frac{b_x}{s_1} {1x}\rangle

In first possibility, after the KK, quantum state becomes

∑ x∈{0,1} n−1a xs 0K(0x⟩) =∑ x∈{0,1} n−1a xs 0(∑ y∈{0,1} n−10y⟩K 0y,0x+1y⟩K 1y,0x) =∑ y∈{0,1} n−10y⟩(∑ x∈{0,1} n−1a xs 0K 0y,0x)+1y⟩(∑ x∈{0,1} n−1a xs 0K 1y,0x)\begin{aligned}&\sum_{x \in \{0,1\}^{n-1}} \frac{a_x}{s_0} K({0x}\rangle) \\&= \sum_{x \in \{0,1\}^{n-1}} \frac{a_x}{s_0} \left(\sum_{y \in \{0,1\}^{n - 1}} {0y}\rangle K_{0y,0x} + {1y}\rangle K_{1y,0x} \right) \\&= \sum_{y \in \{0,1\}^{n - 1}} {0y}\rangle \left( \sum_{x \in \{0,1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x} \right) + {1y}\rangle \left( \sum_{x \in \{0,1\}^{n - 1}} \frac{a_x}{s_0} K_{1y,0x} \right) \end{aligned}

So probability at 0y⟩{0y}\rangle is

∣∑ x∈{0,1} n−1a xs 0K 0y,0x∣ 2\begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x}\end{vmatrix}^2

In second possibility, after the KK, quantum state becomes

∑ x∈{0,1} n−1b xs 1K(1x⟩) =∑ x∈{0,1} n−1b xs 1(∑ y∈{0,1} n−10y⟩K 0y,1x+1y⟩K 1y,1x) =∑ y∈{0,1} n−10y⟩(∑ x∈{0,1} n−1b xs 1K 0y,1x)+1y⟩(∑ x∈{0,1} n−1b xs 1K 1y,1x)\begin{aligned}&\sum_{x \in \{0,1\}^{n-1}} \frac{b_x}{s_1} K({1x}\rangle) \\&= \sum_{x \in \{0,1\}^{n-1}} \frac{b_x}{s_1} \left(\sum_{y \in \{0,1\}^{n - 1}} {0y}\rangle K_{0y,1x} + {1y}\rangle K_{1y,1x} \right) \\&= \sum_{y \in \{0,1\}^{n - 1}} {0y}\rangle \left( \sum_{x \in \{0,1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x} \right) + {1y}\rangle \left( \sum_{x \in \{0,1\}^{n - 1}} \frac{b_x}{s_1} K_{1y,1x} \right) \end{aligned}

So probability at 0y⟩{0y}\rangle is

∣∑ x∈{0,1} n−1b xs 1K 0y,1x∣ 2\begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x}\end{vmatrix}^2

So the overall probability at 0y⟩{0y}\rangle is

s 0 2∣∑ x∈{0,1} n−1a xs 0K 0y,0x∣ 2+s 1 2∣∑ x∈{0,1} n−1b xs 1K 0y,1x∣ 2 =∣∑ x∈{0,1} n−1a xK 0y,0x∣ 2+∣∑ x∈{0,1} n−1b xK 0y,1x∣ 2\begin{aligned}&s_0^2 \begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x}\end{vmatrix}^2 + s_1^2 \begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x}\end{vmatrix}^2 \\&= \begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} a_x K_{0y,0x}\end{vmatrix}^2 + \begin{vmatrix}\sum_{x \in \{0,1\}^{n - 1}} b_x K_{0y,1x}\end{vmatrix}^2\end{aligned}

Not necessarily the same as that of case 1

Case 3 Add additional qbit as the target of control-X of 1st qbit, then immediately measure this n+1n+1 th qbit.

The quantum state after the control-X gate becomes

∑ x∈{0,1} n−1a x0x0⟩+b x1x1⟩\sum_{x \in \{0 , 1\}^{n - 1}} a_x {0x0}\rangle + b_x {1x1}\rangle

After measure the n+1n+1 qbit, it becomes two quantum states with probability s 0 2s_0^2 or s 1 2s_1^2 :

∑ x∈{0,1} n−1a xs 00x0⟩\sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} {0x0}\rangle

or

∑ x∈{0,1} n−1b xs 11x1⟩\sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} {1x1}\rangle

In first possibility, after the KK for the 1 to n qbits, quantum state becomes

∑ x∈{0,1} n−1a xs 0K(0x⟩)0⟩ =∑ x∈{0,1} n−1a xs 0(∑ y∈{0,1} n−10y⟩K 0y,0x+1y⟩K 1y,0x)⟩0 =∑ y∈{0,1} n−10y0⟩(∑ x∈{0,1} n−1a xs 0K 0y,0x)+1y0⟩(∑ x∈{0,1} n−1a xs 0K 1y,0x)\begin{aligned}&\sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} K({0x}\rangle) {0}\rangle \\&= \sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} \left( \sum_{y \in \{0 , 1\}^{n - 1}} {0y}\rangle K_{0y,0x} + {1y}\rangle K_{1y,0x} \right) \rangle{0} \\&= \sum_{y \in \{0 , 1\}^{n - 1}} {0y0}\rangle \left( \sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x} \right) + {1y0}\rangle \left( \sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} K_{1y,0x} \right)\end{aligned}

So probability at 0y⟩{0y}\rangle which can only be with 0y0⟩{0y0}\rangle is

∣∑ x∈{0,1} n−1a xs 0K 0y,0x∣ 2\begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x}\end{vmatrix}^2

In second possibility, after the KK for the 1 to n qbits, quantum state becomes

∑ x∈{0,1} n−1b xs 1K(1x⟩)1⟩ =∑ x∈{0,1} n−1b xs 1(∑ y∈{0,1} n−10y⟩K 0y,1x+1y⟩K 1y,1x)1⟩ =∑ y∈{0,1} n−10y1⟩(∑ x∈{0,1} n−1b xs 1K 0y,1x)+1y1⟩(∑ x∈{0,1} n−1b xs 1K 1y,1x)\begin{aligned}&\sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} K({1x}\rangle) {1}\rangle \\&= \sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} \left( \sum_{y \in \{0 , 1\}^{n - 1}} {0y}\rangle K_{0y,1x} + {1y}\rangle K_{1y,1x} \right) {1}\rangle \\&= \sum_{y \in \{0 , 1\}^{n - 1}} {0y1}\rangle \left( \sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x} \right) + {1y1}\rangle \left( \sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} K_{1y,1x} \right)\end{aligned}

So probability at 0y⟩{0y}\rangle which can only be with 0y1⟩{0y1}\rangle is

∣∑ x∈{0,1} n−1b xs 1K 0y,1x∣ 2\begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x}\end{vmatrix}^2

So at the final measure, the probability at 0y⟩{0y}\rangle is

s 0 2∣∑ x∈{0,1} n−1a xs 0K 0y,0x∣ 2+s 1 2∣∑ x∈{0,1} n−1b xs 1K 0y,1x∣ 2=∣∑ x∈{0,1} n−1a xK 0y,0x∣ 2+∣∑ x∈{0,1} n−1b xK 0y,1x∣ 2s_0^2 \begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} \frac{a_x}{s_0} K_{0y,0x}\end{vmatrix}^2 + s_1^2 \begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} \frac{b_x}{s_1} K_{0y,1x}\end{vmatrix}^2 = \begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} a_x K_{0y,0x}\end{vmatrix}^2 + \begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} b_x K_{0y,1x}\end{vmatrix}^2

The same as that of case 2

Case 4 Add additional qbit as the target of control-X of 1st qbit, then apply KK, then measure all n+1n+1 qbits at the final.

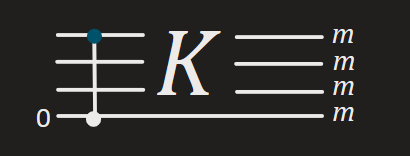
The quantum state after the control-X gate becomes

∑ x∈{0,1} n−1a x0x0⟩+b x1x1⟩\sum_{x \in \{0 , 1\}^{n - 1}} a_x {0x0}\rangle + b_x {1x1}\rangle

After apply KK to 1 to n qbits, the quantum state becomes

∑ x∈{0,1} n−1a xK(0x⟩)0⟩+b xK(1x⟩)1⟩ =∑ x∈{0,1} n−1a x(∑ y∈{0,1} n−10y⟩K 0y,0x+1y⟩K 1y,0x)0⟩+b x(∑ y∈{0,1} n−10y⟩K 0y,1x+1y⟩K 1y,1x)1⟩ =∑ x∈{0,1} n−1∑ y∈{0,1} n−10y0⟩a xK 0y,0x+1y0⟩a xK 1y,0x+0y1⟩b xK 0y,1x+1y1⟩b xK 1y,1x =∑ y∈{0,1} n−10y0⟩(∑ x∈{0,1} n−1a xK 0y,0x)+1y0⟩(∑ x∈{0,1} n−1a xK 1y,0x)+0y1⟩(∑ x∈{0,1} n−1b xK 0y,1x)+1y1⟩(∑ x∈{0,1} n−1b xK 1y,1x)\begin{aligned}&\sum_{x \in \{0 , 1\}^{n - 1}} a_x K({0 x}\rangle) {0}\rangle + b_x K({1 x}\rangle) {1}\rangle\\&= \sum_{x \in \{0 , 1\}^{n - 1}} a_x \left( \sum_{y \in \{0 , 1\}^{n - 1}} {0y}\rangle K_{0y,0x} + {1y}\rangle K_{1y,0x} \right) {0}\rangle + b_x \left( \sum_{y \in \{0 , 1\}^{n - 1}} {0y}\rangle K_{0y,1x} + {1y}\rangle K_{1y,1x} \right) {1}\rangle\\&= \sum_{x \in \{0 , 1\}^{n - 1}} \sum_{y \in \{0 , 1\}^{n - 1}} {0y0}\rangle a_x K_{0y,0x} + {1y0}\rangle a_x K_{1 y , 0 x} + {0y1}\rangle b_x K_{0y,1x} + {1y1}\rangle b_x K_{1y,1x}\\&= \sum_{y \in \{0 , 1\}^{n - 1}} {0 y 0}\rangle \left(\sum_{x \in \{0 , 1\}^{n - 1}} a_x K_{0y,0x}\right) + {1 y 0}\rangle \left(\sum_{x \in \{0 , 1\}^{n - 1}} a_x K_{1y,0x}\right) + {0 y 1}\rangle \left(\sum_{x \in \{0 , 1\}^{n - 1}} b_x K_{0y,1x}\right) + {1 y 1}\rangle \left(\sum_{x \in \{0 , 1\}^{n - 1}} b_x K_{1y,1x}\right)\end{aligned}

State 0y⟩{0y}\rangle comes from 0y0⟩{0y0}\rangle and 0y1⟩{0y1}\rangle so its probability is

∣∑ x∈{0,1} n−1a xK 0y,0x∣ 2+∣∑ x∈{0,1} n−1b xK 0y,1x∣ 2\begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} a_x K_{0y,0x}\end{vmatrix}^2 + \begin{vmatrix}\sum_{x \in \{0 , 1\}^{n - 1}} b_x K_{0y,1x}\end{vmatrix}^2

The same as that of case 2.

In summary, unless KK is some special form, the probability for 0y⟩{0y}\rangle, as well as any 1 to n qbits state, is the same for case 2, case 3, case 4, and is different for case 1.