StructureOfRandomVariables

HomePage | Memberswill go by tor | RecentChanges | Join |

給定 NN 個具有限狀態的隨機變數 X 1,X 2,⋯,X NX_1,X_2, \cdots ,X_N ，第 1⋯N1\cdots N 個隨機變數分別出現在狀態 a 1∈{1⋯A 1},a 2∈{1⋯A 2},⋯,a N∈{1⋯A N}a_1 \in \{1 \cdots A_1 \}, a_2 \in \{ 1 \cdots A_2 \}, \cdots ,a_N \in \{ 1 \cdots A_N \} 的機率記做 Pr(1:a 1,2:a 2,⋯N:a N)\Pr( 1 : a_1,2 : a_2,\cdots N : a_N ) 。如果這N個隨機變數有一個有 KK 個狀態的"共同原因"分別出現在狀態 1⋯K1 \cdots K 有機率 s 1,s 2,⋯s Ks_1,s_2,\cdots s_K ，而且確定發生在某個狀態之後，這 NN 個隨機變數彼此就完全獨立，也就是：

Pr(1:a 1,2:a 2,⋯N:a N)=∑ k=1⋯Ks kPr(1:a 1|S=k)Pr(2:a 2|S=k)⋯Pr(N:a N|S=k)\Pr(1: a_1,2: a_2 ,\cdots N : a_N) = \sum_{k = 1 \cdots K} s_k \Pr(1 : a_1 | S = k ) \Pr( 2 : a_2 | S = k ) \cdots \Pr( N : a_N | S = k )                                 ( 1 )

則稱這 NN 個隨機變數為伴獨立隨機變數．

問題一

NN 個獨立的隨機變數就是只有一個狀態的共同原因的伴獨立隨機變數。

Ans： K=1K=1 的時候 (1) 變成： Pr(1:a 1,2:a 2,⋯N:a N)=Pr(1:a 1|S=1)Pr(2:a 2|S=1)⋯Pr(N:a N|S=1)\Pr(1 : a_1,2 : a_2,\cdots N : a_N) = \Pr( 1 : a_1 | S = 1 ) \Pr( 2 : a_2 | S = 1 ) \cdots \Pr( N : a_N | S = 1 )

問題二

任意NN 個隨機變數一定存在一個伴獨立結構。

Ans: 任意 NN 個隨機變數都可以是共同原因狀態數 K=A 1A 2⋯A NK = A_1 A_2 \cdots A_N 的伴獨立結構。在每個共同原因之下這 NN 個隨機變數有 100% 的機率發生在特定狀態。例如 N=2,A 1=A 2=2N =2,A_1 = A_2 = 2 ：

[p 11 p 12 p 21 p 22]=p 11[1 0][1 0]+p 12[1 0][0 1]+p 21[0 1][1 0]+p 22[0 1][0 1]\begin{bmatrix}p_{11}&p_{12}\\p_{21}&p_{22}\end{bmatrix} = p_{11} \begin{bmatrix}1\\0\end{bmatrix}\begin{bmatrix}1&0\end{bmatrix} + p_{12} \begin{bmatrix}1\\0\end{bmatrix}\begin{bmatrix}0&1\end{bmatrix} + p_{21} \begin{bmatrix}0\\1\end{bmatrix}\begin{bmatrix}1&0\end{bmatrix} + p_{22} \begin{bmatrix}0\\1\end{bmatrix}\begin{bmatrix}0&1\end{bmatrix}

由問題二可知伴獨立結構隨機變數的範圍和隨機變數的範圍一樣大，而且未必具有 ∏ n=1 NA n−1\prod_{n = 1}^N A_n - 1 這麼多的自由度資訊，只是最少共同原因狀態數的伴獨立結構未必容易找。

如果 NN 個隨機變數的機率數值有 NN 個參數，Pr(1:a 1,2:a 2,⋯N:a N;α 1,α 2,⋯α N)\Pr(1 : a_1,2 : a_2 ,\cdots N : a_N ;\alpha_1,\alpha_2,\cdots \alpha_N) ，但是這些參數卻與共同原因無關，只是在地 (locality) 的隨機變數的控制參數，也就是可以拆解成：

Pr(n:a n;α n) =∑ ks kPr(n:a n;α n|S=k) Pr(1:a 1,2:a 2,⋯N:a N;α 1,α 2,⋯α N) =∑ ks kPr(1:a 1;α 1|S=k)Pr(2:a 2;α 2|S=k)⋯Pr(N:a N;α N|S=k)\begin{aligned}\Pr(n : a_n ;\alpha_n) &= \sum_k s_k \Pr( n : a_n;\alpha_n | S = k )\\\Pr(1 : a_1,2 : a_2 ,\cdots N : a_N ;\alpha_1 ,\alpha_2 ,\cdots \alpha_N) &= \sum_k s_k \Pr(1 : a_1;\alpha_1 | S = k) \Pr( 2 : a_2;\alpha_2 | S = k ) \cdots \Pr( N : a_N;\alpha_N | S = k )\end{aligned}                                                ( 2 )

則稱此 NN 隨機變數為局部參數隨機變數；變動第一個隨機變數 X 1X_1 的參數 α 1\alpha_1 不會影響到其他隨機變數，要模擬第一個隨機變數也不需要除了 α 1\alpha_1 以外的其他隨機變數的參數。

以下說明給定 Pr(1:a 1,2:a 2,⋯N:a N;α 1,α 2,⋯α N)\Pr(1 : a_1,2 : a_2,\cdots N : a_N ;\alpha_1,\alpha_2,\cdots \alpha_N) 後，可能的話如何找出具有儘可能少狀態的共同原因而且有此局部控制參數的伴獨立結構。

一個正常的函數在一個區間都可以 basis 函數列展開，展開後的係數不會有兩套，常用的 basis 函數列有 也就是泰勒展開，或者 1,cos(α),sin(α),cos 2(α),sin 2(α),⋯1,\alpha ,\alpha^2 ,  \cdots1,\cos(\alpha), \sin(\alpha), \cos^2(\alpha), \sin^2(\alpha),\cdots 也就是傅立葉展開。這邊以 f 0(α)=1,f 1(α),f 2(α),⋯f_0(\alpha) = 1,f_1(\alpha),f_2(\alpha) , \cdots 表示這些 basis 函數，Pr(n:a n;α n|S=k)\Pr(n : a_n;\alpha_n | S = k ) 展開的係數為 X nka niX_{n k a_n i} ，也就是：

Pr(n:a n;α n|S=k)=∑ iX nka ni⋅f i(α n)\Pr(n : a_n; \alpha_n| S = k) = \sum_i X_{n k a_n i} \cdot f_i (\alpha_n)                                                   ( 3 )

因此：

Pr(1:a 1,2:a 2,⋯N:a N;α 1,α 2,⋯α N) =∑ ks k∑ i 1X 1ka 1i 1f i 1(α 1)∑ i 2X 2ka 2i 2f i 2(α 2)⋯∑ i NX Nka Ni Nf i N(α N) =∑ i 1,i 2,⋯i N∑ ks kX 1ka 1i 1X 2ka 2i 2⋯X Nka Ni Nf i 1(α 1)f i 2(α 2)⋯f i N(α N)\begin{aligned}&\Pr(1 : a_1 ,2 : a_2 ,\cdots N : a_N ;\alpha_1,\alpha_2,\cdots \alpha_N)\\&= \sum_k s_k \sum_{i_1} X_{1 k a_1 i_1} f_{i_1}(\alpha_1) \sum_{i_2} X_{2 k a_2 i_2} f_{i_2}(\alpha_2) \cdots \sum_{i_N} X_{N k a_N i_N} f_{i_N}(\alpha_N)\\&= \sum_{i_1 , i_2 , \cdots i_N} \sum_k s_k X_{1 k a_1 i_1} X_{2 k a_2 i_2} \cdots X_{N k a_N i_N} f_{i_1}(\alpha_1) f_{i_2}(\alpha_2) \cdots f_{i_N}(\alpha_N)\end{aligned}                                 (4)

計算一下未知數和方程式的個數。以 M nM_n 代表第 nn 個隨機變數以 basis 函數展開的項數，因此 (4) 有 ∏ n=1 NA nM n\prod_{n = 1}^N A_n M_n 個方程式。

由 (3) 所以有：

1=∑ a nPr(n:a n;α n|S=k)=∑ i∑ a nX nka nif i(α n)1 = \sum_{a_n} \Pr(n : a_n;\alpha_n |S = k) = \sum_i \sum_{a_n} X_{n k a_n i} f_i(\alpha_n)

所以有：

1 i=0=∑ a nX nka ni1_{i=0} = \sum_{a_ n} X_{n k a_n i}                                                                                 ( 5 )

所以 (5) 有 K∑ n=1 NM nK \sum_{n = 1}^N M_n 個方程式。

由 (4) (5) 的方程式，因為

1=∑ a 1⋯a nPr(1:a 1,2:a 2,⋯N:a N;α 1,α 2,⋯α N)=∑ ks k1 = \sum_{a_1 \cdots a_n} \Pr(1 : a_1 ,2 : a_2 ,\cdots N : a_N ;\alpha_1 ,\alpha_2 ,\cdots \alpha_N) = \sum_k s_k

，所以： ∑ ks k=1\sum_k s_k = 1 已經自動滿足，不用額外設定條件，所以方程式部分總共有 K∑ n=1 NM n+∏ n=1 NA nM nK \sum_{n = 1}^N M_n + \prod_{n = 1}^N A_n M_n 個。

未知數部分，由 (3) 總共有 K∑ n=1 NA nM nK \sum_{n = 1}^N A_n M_n 個，加上共同原因的狀態的機率 KK 個，總共有 K⋅(1+∑ n=1 NA nM n)K \cdot \left(1 + \sum_{n = 1}^N A_n M_n\right) 個。

因此共同原因的狀態個數，在沒有特殊情況下，需滿足：

K⋅(1+∑ n=1 NA nM n)≥K∑ n=1 NM n+∏ n=1 NA nM nK \cdot \left(1 + \sum_{n = 1}^N A_n M_n \right) \geq K \sum_{n = 1}^N M_n + \prod_{n = 1}^N A_n M_n

也就是

K≥∏ n=1 NA nM n1+∑ n=1 N(A n−1)M nK \geq \frac{\prod_{n = 1}^N A_n M_n}{1 + \sum_{n = 1}^N (A_n - 1) M_n}

問題三

有兩個只有兩個狀態的隨機變數，p 11=0.2,p 21=0.2,p 12=0.5,p 22=0.1p_{11} = 0.2 ,p_{21} = 0.2,p_{12} = 0.5 , p_{22} = 0.1 ，除了問題二的無聊拆法以外，拆解出一個它們的伴獨立結構。

Ans： 因為 N=2,M 1=M 2=1,A 1=A 2=2N = 2,M_1 = M_2 = 1 , A_1 = A_2 = 2 ，所以 K≥2⋅21+(2−1)1+(2−1)1=1.33K \geq \frac{2 \cdot 2}{1 + (2 - 1) 1 + (2 - 1) 1} = 1.33 ，所以假設共同原因有兩個狀態，用 Excel 規劃求解得出：

[0.2 0.5 0.2 0.1]=0.325223⋅[0.077556 0.922444][0.666667 0.333333]+0.674777⋅[1 0][0.271474 0.728526]\begin{bmatrix}0.2&0.5\\0.2&0.1\end{bmatrix} = 0.325223 \cdot \begin{bmatrix}0.077556\\0.922444\end{bmatrix} \begin{bmatrix}0.666667&0.333333\end{bmatrix} + 0.674777 \cdot \begin{bmatrix}1\\0\end{bmatrix} \begin{bmatrix}0.271474&0.728526\end{bmatrix}

也就是共同原因有 0.325223 的機率發生在第一個狀態，有 0.674777 的機率發生在第二個狀態。當共同原因是第一個狀態的時候，第一個隨機變數和第二個隨機變數獨立分別有 0.077556 和 0.666667 的機率出現在各自的第一個狀態。當共同原因是第二個狀態的時候，第一個隨機變數和第二個隨機變數獨立分別有 1.0 和 0.271474 的機率出現在各自的第一個狀態。

問題四

兩個只有兩個狀態的隨機變數的機率是 p 11=12sin 2(α 1−α 2),p 21=12cos 2(α 1−α 2),p 12=12cos 2(α 1−α 2),p 22=12sin 2(α 1−α 2)p_{11} = \frac{1}{2} \sin^2(\alpha_1 - \alpha_2),p_{21} = \frac{1}{2} \cos^2( \alpha_1 - \alpha_2 ) ,p_{12} = \frac{1}{2} \cos^2( \alpha_1 - \alpha_2 ), p_{22} = \frac{1}{2} \sin^2( \alpha_1 - \alpha_2 ) ，試圖去拆解出它們並證明它們不可能是局部參數隨機變數。

Ans：

12sin 2(α 1−α 2) =14(1−cos(2(α 1−α 2))) =0.25−0.25cos(2α 1)cos(2α 2)−0.25sin(2α 1)sin(2α 2) 12cos 2(α 1−α 2) =0.25+0.25cos(2α 1)cos(2α 2)+0.25sin(2α 1)sin(2α 2)\begin{aligned}\frac{1}{2} \sin^2(\alpha_1 - \alpha_2) &= \frac{1}{4}\left(1 - \cos(2(\alpha_1 - \alpha_2))\right)\\&= 0.25 - 0.25 \cos(2 \alpha_1) \cos(2 \alpha_2) - 0.25 \sin(2 \alpha_1) \sin(2 \alpha_2)\\\frac{1}{2} \cos^2(\alpha_1 - \alpha_2) &= 0.25 + 0.25 \cos(2 \alpha_1) \cos(2 \alpha_2) + 0.25 \sin(2 \alpha_1) \sin(2 \alpha_2)\end{aligned}

所以這裡用傅立葉展開最自然，三個 basis 函數是 1,cos(2α),sin(2α)1,\cos(2\alpha),\sin(2\alpha)。因為 N=2,M 1=M 2=3,A 1=A 2=2N = 2,M_1 = M_2 = 3 , A_1 = A_2 = 2 ，所以 K≥6⋅61+(2−1)3+(2−1)3=5.14K \geq \frac{6 \cdot 6}{1 + (2 - 1) 3 + (2 - 1) 3} = 5.14 ，所以需要六個狀態的共同原因。

注意到機率的分配指出第一個隨機變數和第二個隨機變數對稱。

在(4)裡面有這二個方程式：

−0.25=∑ ks kX 1k11X 2k11=∑ ks kX 1k12X 2k12-0.25 = \sum_k s_k X_{1 k 11} X_{2 k 11} = \sum_k s_k X_{1 k 12} X_{2 k 12}

所以有： (6)

0.25 =|∑ ks kX 1k11X 2k11|≤∑ ks kX 1k11 2∑ ks kX 2k11 2 0.25 =|∑ ks kX 1k12X 2k12|≤∑ ks kX 1k12 2∑ ks kX 2k12 2\begin{aligned}0.25 &= \vert \sum_k s_k X_{1 k 11} X_{2 k 11} \vert \leq \sqrt{\sum_k s_k X_{1 k 11}^2} \sqrt{\sum_k s_k X_{2 k 11}^2}\\0.25 &= \vert \sum_k s_k X_{1 k 12} X_{2 k 12} \vert \leq \sqrt{\sum_k s_k X_{1 k 12}^2} \sqrt{\sum_k s_k X_{2 k 12}^2}\end{aligned}

另一方面因為 Pr(1:1;α 1|S=k)≥0\Pr(1 : 1;\alpha_1| S = k) \geq 0 ，而且 X 1k11cos(2α 1)+X 1k12sin(2α 1)X_{1 k 11} \cos(2 \alpha_1) + X_{1 k 12} \sin(2 \alpha_1) 的最小值是 −X 1k11 2+X 1k12 2-\sqrt{X_{1 k 11}^2 + X_{1 k 12}^2} ，所以 X 1k10≥X 1k11 2+X 1k12 2X_{1 k 10} \geq \sqrt{X_{1 k 11}^2 + X_{1 k 12}^2}

在(4)裡面有這二個方程式：

−0.25=∑ ks kX 1k21X 2k21=∑ ks kX 1k22X 2k22-0.25 = \sum_k s_k X_{1 k 21} X_{2 k 21} = \sum_k s_k X_{1 k 22} X_{2 k 22}

所以有：

0.25 =|∑ ks kX 1k21X 2k21|≤∑ ks kX 1k21 2∑ ks kX 2k21 2=∑ ks kX 1k21 2 0.25 =|∑ ks kX 1k22X 2k22|≤∑ ks kX 1k22 2∑ ks kX 2k22 2=∑ ks kX 1k22 2\begin{aligned}0.25 &= \vert \sum_k s_k X_{1 k 21} X_{2 k 21} \vert \leq \sqrt{\sum_k s_k X_{1 k 21}^2} \sqrt{\sum_k s_k X_{2 k 21}^2} = \sum_k s_k X_{1 k 21}^2\\0.25 &= \vert \sum_k s_k X_{1 k 22} X_{2 k 22} \vert \leq \sqrt{\sum_k s_k X_{1 k 22}^2} \sqrt{\sum_k s_k X_{2 k 22}^2} = \sum_k s_k X_{1 k 22}^2\end{aligned}

另一方面因為 Pr(1:2;α 1|S=k)≥0\Pr(1 : 2;\alpha_1| S = k) \geq 0 ，而且 X 1k21cos(2α 1)+X 1k22sin(2α 1)X_{1 k 21} \cos(2 \alpha_1) + X_{1 k 22} \sin(2 \alpha_1) 的最小值是 −X 1k21 2+X 1k22 2-\sqrt{X_{1 k 21}^2 + X_{1 k 22}^2} ，所以 X 1k20≥X 1k21 2+X 1k22 2X_{1 k 20} \geq \sqrt{X_{1 k 21}^2 + X_{1 k 22}^2}

所以由 (5) 裡面的 1=X 1k10+X 1k201 = X_{1 k 10} + X_{1 k 20} 和 X 1k21=−X 1k11X_{1 k 21}= - X_{1 k 11} 和 X 1k22=−X 1k12X_{1 k 22} = - X_{1 k 12}

1=X 1k10+X 1k20≥X 1k11 2+X 1k12 2+X 1k21 2+X 1k22 2=2X 1k11 2+X 1k12 21 = X_{1 k 10} + X_{1 k 20} \geq \sqrt{X_{1 k 11}^2 + X_{1 k 12}^2} + \sqrt{X_{1 k 21}^2 + X_{1 k 22}^2} = 2 \sqrt{X_{1 k 11}^2 + X_{1 k 12}^2}

所以有： 0.25≥X 1k11 2+X 1k12 20.25 \geq X_{1 k 11}^2 + X_{1 k 12}^2

所以

0.25=0.25∑ ks k≥∑ ks k(X 1k11 2+X 1k12 2)>∑ ks kX 1k11 20.25 = 0.25 \sum_k s_k \geq \sum_k s_k ( X_{1 k 11}^2 + X_{1 k 12}^2 ) > \sum_k s_k X_{1 k 11}^2

同理，

0.25>∑ ks kX 2k11 20.25 > \sum_k s_k X_{2 k 11}^2

所以有： 0.25>∑ ks kX 1k11 2∑ ks kX 2k11 20.25 > \sqrt{\sum_k s_k X_{1 k 11}^2} \sqrt{\sum_k s_k X_{2 k 11}^2}

但是和 (6) 矛盾，所以即使拆解完成，一定也有某一個狀態的時候會有不合理的負機率。試著去Excel裡規劃求解去找解，得到（黑體部分是自由變數，其他的變數由拘束條件被間接決定）：

N=2 K=6 M 1=M 2=3 A 1=A 2=2 i n=0:1 n=1 n=2 i n=1:cos(2α) i n=0 i n=1 i n=2 i n=0 i n=1 i n=2 i n=2:sin(2α) s k a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 k=1 0.166667 0.5 0.5 0.235030 −0.235030 0.121104 −0.121104 0.5 0.5 −0.235030 0.235030 −0.121104 0.121104 k=2 0.166667 0.5 0.5 0.169099 −0.169099 −0.971488 0.971488 0.5 0.5 −0.169099 0.169099 0.971488 −0.971488 k=3 0.166667 0.5 0.5 0.217407 −0.217407 0.068368 −0.068368 0.5 0.5 −0.217407 0.217407 −0.068368 0.068368 k=4 0.166667 0.5 0.5 −1.116347 1.116347 0.059298 −0.059298 0.5 0.5 1.116347 −1.116347 −0.059298 0.059298 k=5 0.166667 0.5 0.5 0.236100 −0.236100 −0.007554 0.007554 0.5 0.5 −0.236100 0.236100 0.007554 −0.007554 k=6 0.166667 0.5 0.5 0.258711 −0.258711 0.730273 −0.730273 0.5 0.5 −0.258711 0.258711 −0.730273 0.730273\begin{array}{lllllllllllll}\begin{aligned}N=2\\K=6\\M_1=M_2=3\\A_1=A_2=2\end{aligned}&&&&&&&&&&&&&\\i_n=0:1&&n=1&&&&&&n=2&&&&&\\i_n=1:\cos(2 \alpha)&&i_n=0&&i_n=1&&i_n=2&&i_n=0&&i_n=1&&i_n=2&\\i_n=2:\sin(2 \alpha)&s_k&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2\\k=1&0.166667&0.5&0.5&0.235030&-0.235030&0.121104&-0.121104&0.5&0.5&-0.235030&0.235030&-0.121104&0.121104\\k=2&0.166667&0.5&0.5&0.169099&-0.169099&-0.971488&0.971488&0.5&0.5&-0.169099&0.169099&0.971488&-0.971488\\k=3&0.166667&0.5&0.5&0.217407&-0.217407&0.068368&-0.068368&0.5&0.5&-0.217407&0.217407&-0.068368&0.068368\\k=4&0.166667&0.5&0.5&-1.116347&1.116347&0.059298&-0.059298&0.5&0.5&1.116347&-1.116347&-0.059298&0.059298\\k=5&0.166667&0.5&0.5&0.236100&-0.236100&-0.007554&0.007554&0.5&0.5&-0.236100&0.236100&0.007554&-0.007554\\k=6&0.166667&0.5&0.5&0.258711&-0.258711&0.730273&-0.730273&0.5&0.5&-0.258711&0.258711&-0.730273&0.730273\end{array}

個別共同原因下的 Pr(1:1;α 1|k)\Pr(1 : 1;\alpha_1 |k ) 圖形為：

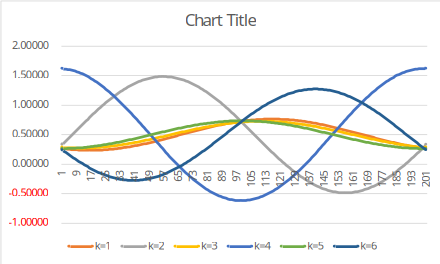
這個拆解因為問題本身的對稱性其實共同原因的狀態數可以更少，例如只有三個狀態的共同原因：

N=2 K=3 M 1=M 2=3 A 1=A 2=2 i n=0:1 n=1 n=2 i n=1:cos(2α) i n=0 i n=1 i n=2 i n=0 i n=1 i n=2 i n=2:sin(2α) s k a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 k=1 0.000000 −0.1 1.1 −0.008206 0.008206 −0.011387 0.011387 −0.1 1.1 0.008206 −0.008206 0.011387 −0.011387 k=2 0.000000 0.0 1.05 0.008138 −0.008138 0.011429 −0.011429 0.0 1.05 −0.008138 0.008138 −0.011429 0.011429 k=3 0.000000 0.0 1.04 −0.796622 0.796622 −4.260839 4.260839 0.0 1.04 0.796622 −0.796622 4.260839 −4.260839 k=4 0.333333 0.5 0.5 0.688011 −0.688011 0.163218 −0.163218 0.5 0.5 −0.688011 0.688011 −0.163218 0.163218 k=5 0.333333 0.5 0.5 −0.485356 0.485356 0.514226 −0.514226 0.5 0.5 0.485356 −0.485356 −0.514226 0.514226 k=6 0.333333 0.5 0.5 −0.202655 0.202655 −0.677444 0.677444 0.5 0.5 0.202655 −0.202655 0.677444 −0.677444\begin{array}{lllllllllllll}\begin{aligned}N=2\\K=3\\M_1=M_2=3\\A_1=A_2=2\end{aligned}&&&&&&&&&&&&&\\i_n=0:1&&n=1&&&&&&n=2&&&&&\\i_n=1:\cos(2 \alpha)&&i_n=0&&i_n=1&&i_n=2&&i_n=0&&i_n=1&&i_n=2&\\i_n=2:\sin(2 \alpha)&s_k&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2\\k=1&0.000000&-0.1&1.1&-0.008206&0.008206&-0.011387&0.011387&-0.1&1.1&0.008206&-0.008206&0.011387&-0.011387\\k=2&0.000000&0.0&1.05&0.008138&-0.008138&0.011429&-0.011429&0.0&1.05&-0.008138&0.008138&-0.011429&0.011429\\k=3&0.000000&0.0&1.04&-0.796622&0.796622&-4.260839&4.260839&0.0&1.04&0.796622&-0.796622&4.260839&-4.260839\\k=4&0.333333&0.5&0.5&0.688011&-0.688011&0.163218&-0.163218&0.5&0.5&-0.688011&0.688011&-0.163218&0.163218\\k=5&0.333333&0.5&0.5&-0.485356&0.485356&0.514226&-0.514226&0.5&0.5&0.485356&-0.485356&-0.514226&0.514226\\k=6&0.333333&0.5&0.5&-0.202655&0.202655&-0.677444&0.677444&0.5&0.5&0.202655&-0.202655&0.677444&-0.677444\end{array}

個別共同原因下的 Pr(1:1;α 1|k)\Pr(1 : 1;\alpha_1| k) 圖形為：

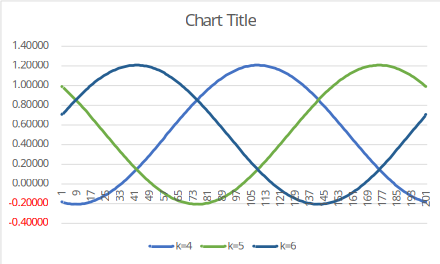
由這個圖可以猜測有一個解是長這個樣子：

K≥3 s k=1K X 1k11=−X 1k21=−X 2k11=X 2k21=r⋅cos(θ+2πKk) X 1k12=−X 1k22=−X 2k12=X 2k22=r⋅sin(θ+2πKk)\begin{aligned}&K \geq 3\\&s_k = \frac{1}{K}\\&X_{1 k 11} = - X_{1 k 21} = - X_{2 k 11} = X_{2 k 21} = r \cdot \cos(\theta + \frac{2 \pi}{K} k)\\&X_{1 k 12} = - X_{1 k 22} = - X_{2 k 12} = X_{2 k 22} = r \cdot \sin(\theta + \frac{2 \pi}{K} k)\end{aligned}

由 0=∑ ks kX 1k11X 2k120 = \sum_k s_k X_{1 k 11} X_{2 k 12} 得到 θ\theta 可以是任意值。

−0.25=∑ ks kX 1k11X 2k11-0.25 = \sum_k s_k X_{1 k 11} X_{2 k 11} 得到 r=12r = \frac{1}{\sqrt{2}}

如果 NN 個隨機變數是局部參數隨機變數，所以可以一個參數一行的實驗方式記錄下這些隨機變數的實現狀態，也就是這樣的實驗結果紀錄表：

Experiment Settings: X 1(α 1) X 2(α 2) ⋯ X N(α N) #1 * * ⋯ * #2 * * ⋯ * ⋮ ⋮ ⋮ ⋮ ⋮\begin{array}{llll}\text{Experiment Settings:}&X_1(\alpha_1)&X_2(\alpha_2)&\cdots&X_N(\alpha_N)\\#1&\ast&\ast&\cdots&\ast\\#2&\ast&\ast&\cdots&\ast\\\vdots&\vdots&\vdots&\vdots&\vdots\end{array}

把每個隨機變數的狀態分成兩群，稱之為 HH 群和 TT 群。例如一種分法，HH 群是 1 和 2，TT 群是 3⋯3 \cdots ，或者，HH 群是 1，TT 群是 2⋯2 \cdots 。

在每一列實驗結果裡，因為根據簡單的邏輯，如果

  • X 1(α 1)X_1 ( \alpha_1 ) 和 X 2(α 2)X_2 ( \alpha_2 ) 不同群
  • X 2(α 2)X_2 ( \alpha_2 ) 和 X 3(α 3)X_3 ( \alpha_3 ) 不同群
  • X 3(α 3)X_3 ( \alpha_3 ) 和 X 4(α 4)X_4 ( \alpha_4 ) 不同群
  • ⋯\cdots

則一定有：當 NN 是奇數 X 1(α 1)X_1 ( \alpha_1 ) 一定和 X N(α N)X_N ( \alpha_N ) 是同一群，當 NN 是偶數 X 1(α 1)X_1 ( \alpha_1 ) 一定和 X N(α N)X_N ( \alpha_N ) 不是同一群。也就是說，當 NN 是奇數有：如果 X 1(α 1)X_1 ( \alpha_1 ) 和 X N(α N)X_N ( \alpha_N ) 不是同一群，則 X 1(α 1)X_1 ( \alpha_1 ) 和 X 2(α 2)X_2 ( \alpha_2 ) 是同群或者 X 2(α 2)X_2 ( \alpha_2 ) 和 X 3(α 3)X_3 ( \alpha_3 ) 是同群或者 X 3(α 3)X_3 ( \alpha_3 ) 和 X 4(α 4)X_4 ( \alpha_4 ) 是同群或者 ⋯\cdots。當 NN 是偶數有：如果 X 1(α 1)X_1 ( \alpha_1 ) 和 X N(α N)X_N ( \alpha_N ) 是同一群，則 X 1(α 1)X_1 ( \alpha_1 ) 和 X 2(α 2)X_2 ( \alpha_2 ) 是同群或者 X 2(α 2)X_2 ( \alpha_2 ) 和 X 3(α 3)X_3 ( \alpha_3 ) 是同群或者 X 3(α 3)X_3 ( \alpha_3 ) 和 X 4(α 4)X_4 ( \alpha_4 ) 是同群或者 ⋯\cdots。

因此，當 NN 是奇數：

Pr(X 1(α 1),X N(α N)∉same group)≤∑ n=1 N−1Pr(X n(α n),X n+1(α n+1)∈same group)\Pr(X_1(\alpha_1),X_N(\alpha_N) \notin \text{same group}) \leq \sum_{n=1}^{N-1} \Pr(X_n(\alpha_n),X_{n + 1}(\alpha_{n + 1}) \in \text{same group})

當 NN 是偶數：

Pr(X 1(α 1),X N(α N)∈same group)≤∑ n=1 N−1Pr(X n(α n),X n+1(α n+1)∈same group)\Pr(X_1(\alpha_1),X_N(\alpha_N) \in \text{same group}) \leq \sum_{n=1}^{N-1} \Pr(X_n(\alpha_n),X_{n+1}(\alpha_{n+1}) \in \text{same group})                           ( 7 )

這就是 Bell 不等式。

問題五

用 Bell 不等式證明四個倆倆滿足問題四設定機率的隨機變數不可能是局部參數隨機變數。

Ans： 如果他們是局部參數隨機變數，設定 HH 是1，TT 是2，所以同群的機率是 p 11+p 22=sin 2(α 1−α 2)p_{11}+p_{22}=\sin^2(\alpha_1 - \alpha_2)，不同群的機率是 p 12+p 21=cos 2(α 1−α 2)p_{12}+p_{21}=\cos^2(\alpha_1 - \alpha_2)，所以(α 1,α 2)=(0,π6),(π6,π3),(π3,π2),(0,π2)(\alpha_1,\alpha_2) = (0,\frac{\pi}{6}),(\frac{\pi}{6},\frac{\pi}{3}),(\frac{\pi}{3}, \frac{\pi}{2}),(0,\frac{\pi}{2}) ，(7) 就是 1≤14+14+141 \leq \frac{1}{4} + \frac{1}{4} + \frac{1}{4} 。矛盾。

問題六

兩個只有兩個狀態的隨機變數的機率是：

p 11=p 22=0.25−0.125cos(2α 1)cos(2α 2)−0.125sin(2α 1)sin(2α 2) p 12=p 21=0.25+0.125cos(2α 1)cos(2α 2)+0.125sin(2α 1)sin(2α 2)\begin{aligned}p_{11} = p_{22} = 0.25 - 0.125 \cos(2 \alpha_1) \cos(2 \alpha_2) - 0.125 \sin(2 \alpha_1) \sin(2 \alpha_2)\\p_{12} = p_{21} = 0.25 + 0.125 \cos(2 \alpha_1) \cos(2 \alpha_2) + 0.125 \sin(2 \alpha_1) \sin(2 \alpha_2)\end{aligned}

找出它們的局部參數隨機變數結構。

Ans： 根據問題四最後提到的拆解去稍微修改。只要稍微改 rr 就可以讓全部的方程式還是符合：

−0.125=∑ ks kX 1k11X 2k11-0.125 = \sum_k s_k X_{1 k 11} X_{2 k 11} 得到 r=0.5r = 0.5

N=2 K=6 M 1=M 2=3 A 1=A 2=2 i n=0:1 n=1 n=2 i n=1:cos(2α) i n=0 i n=1 i n=2 i n=0 i n=1 i n=2 i n=2:sin(2α) s k a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 k=1 0.166667 0.5 0.5 0.158990 −0.158990 0.474049 −0.474049 0.5 0.5 −0.158990 0.158990 −0.474049 0.474049 k=2 0.166667 0.5 0.5 −0.331043 0.331043 0.374714 −0.374714 0.5 0.5 0.331043 −0.331043 −0.374714 0.374714 k=3 0.166667 0.5 0.5 −0.490033 0.490033 −0.099335 0.099335 0.5 0.5 0.490033 −0.490033 0.099335 −0.099335 k=4 0.166667 0.5 0.5 −0.158990 0.158990 −0.474049 0.474049 0.5 0.5 0.158990 −0.158990 0.474049 −0.474049 k=5 0.166667 0.5 0.5 0.331043 −0.331043 −0.374714 0.374714 0.5 0.5 −0.331043 0.331043 0.374714 −0.374714 k=6 0.166667 0.5 0.5 0.490033 −0.490033 0.099335 −0.099335 0.5 0.5 −0.490033 0.490033 −0.099335 0.099335\begin{array}{lllllllllllll}\begin{aligned}N=2\\K=6\\M_1=M_2=3\\A_1=A_2=2\end{aligned}&&&&&&&&&&&&&\\i_n=0:1&&n=1&&&&&&n=2&&&&&\\i_n=1:\cos(2 \alpha)&&i_n=0&&i_n=1&&i_n=2&&i_n=0&&i_n=1&&i_n=2&\\i_n=2:\sin(2 \alpha)&s_k&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2\\k=1&0.166667&0.5&0.5&0.158990&-0.158990&0.474049&-0.474049&0.5&0.5&-0.158990&0.158990&-0.474049&0.474049\\k=2&0.166667&0.5&0.5&-0.331043&0.331043&0.374714&-0.374714&0.5&0.5&0.331043&-0.331043&-0.374714&0.374714\\k=3&0.166667&0.5&0.5&-0.490033&0.490033&-0.099335&0.099335&0.5&0.5&0.490033&-0.490033&0.099335&-0.099335\\k=4&0.166667&0.5&0.5&-0.158990&0.158990&-0.474049&0.474049&0.5&0.5&0.158990&-0.158990&0.474049&-0.474049\\k=5&0.166667&0.5&0.5&0.331043&-0.331043&-0.374714&0.374714&0.5&0.5&-0.331043&0.331043&0.374714&-0.374714\\k=6&0.166667&0.5&0.5&0.490033&-0.490033&0.099335&-0.099335&0.5&0.5&-0.490033&0.490033&-0.099335&0.099335\end{array}

此時的個別共同原因下的 Pr(1:1;α 1|k)\Pr(1 : 1;\alpha_1| k) 圖形為：

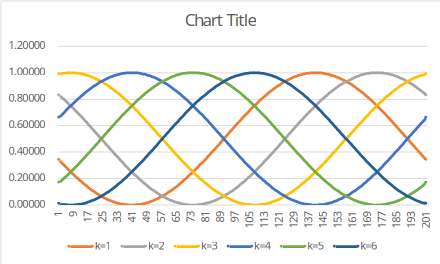
同樣因為問題本身的對稱性，共同原因的狀態數可以是3：

N=2 K=3 M 1=M 2=3 A 1=A 2=2 i n=0:1 n=1 n=2 i n=1:cos(2α) i n=0 i n=1 i n=2 i n=0 i n=1 i n=2 i n=2:sin(2α) s k a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 a n=1 a n=2 k=1 0.000000 0.5 0.5 0.158990 −0.158990 0.474049 −0.474049 0.5 0.5 −0.158990 0.158990 −0.474049 0.474049 k=2 0.000000 0.5 0.5 −0.331043 0.331043 0.374714 −0.374714 0.5 0.5 0.331043 −0.331043 −0.374714 0.374714 k=3 0.000000 0.5 0.5 −0.490033 0.490033 −0.099335 0.099335 0.5 0.5 0.490033 −0.490033 0.099335 −0.099335 k=4 0.333333 0.5 0.5 −0.331043 0.331043 0.374714 −0.374714 0.5 0.5 0.331043 −0.331043 −0.374714 0.374714 k=5 0.333333 0.5 0.5 −0.158990 0.158990 −0.474049 0.474049 0.5 0.5 0.158990 −0.158990 0.474049 −0.474049 k=6 0.333333 0.5 0.5 0.490033 −0.490033 0.099335 −0.099335 0.5 0.5 −0.490033 0.490033 −0.099335 0.099335\begin{array}{lllllllllllll}\begin{aligned}N=2\\K=3\\M_1=M_2=3\\A_1=A_2=2\end{aligned}&&&&&&&&&&&&&\\i_n=0:1&&n=1&&&&&&n=2&&&&&\\i_n=1:\cos(2 \alpha)&&i_n=0&&i_n=1&&i_n=2&&i_n=0&&i_n=1&&i_n=2&\\i_n=2:\sin(2 \alpha)&s_k&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2&a_n=1&a_n=2\\k=1&0.000000&0.5&0.5&0.158990&-0.158990&0.474049&-0.474049&0.5&0.5&-0.158990&0.158990&-0.474049&0.474049\\k=2&0.000000&0.5&0.5&-0.331043&0.331043&0.374714&-0.374714&0.5&0.5&0.331043&-0.331043&-0.374714&0.374714\\k=3&0.000000&0.5&0.5&-0.490033&0.490033&-0.099335&0.099335&0.5&0.5&0.490033&-0.490033&0.099335&-0.099335\\k=4&0.333333&0.5&0.5&-0.331043&0.331043&0.374714&-0.374714&0.5&0.5&0.331043&-0.331043&-0.374714&0.374714\\k=5&0.333333&0.5&0.5&-0.158990&0.158990&-0.474049&0.474049&0.5&0.5&0.158990&-0.158990&0.474049&-0.474049\\k=6&0.333333&0.5&0.5&0.490033&-0.490033&0.099335&-0.099335&0.5&0.5&-0.490033&0.490033&-0.099335&0.099335\end{array}

此時的個別共同原因下的 Pr(1:1;α 1|k)\Pr(1 : 1;\alpha_1 |k) 圖形為：

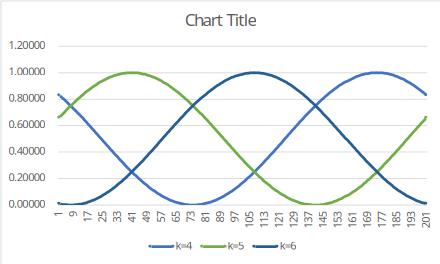
模擬第一個隨機變數的時候不需要知道 α 2\alpha_2 的數值。