交流電路的最終電壓電流

HomePage | Memberswill go by tor | RecentChanges | Join |

交流電的一般解

x tx_t 是 1 乘 n 矩陣，AA 和 CC 是 n 乘 n 矩陣，交流電路總是一開始長這樣：

dx tdtC=x tA+[b 1cos(ωt+p 1) b 2cos(ωt+p 2) ⋯ b ncos(ωt+p n)]\frac{d x_t}{d t} C = x_t A + \begin{bmatrix}b_1 \cos(\omega t + p_1)&b_2 \cos(\omega t + p_2)& \cdots &b_n \cos(\omega t + p_n)\end{bmatrix}

以複數來表達是某個 BB ：

dx tdtC=x tA+e i(ωt+p)B\frac{d x_t}{d t} C = x_t A + e^{i (\omega t + p)} B

如果可以做某些行運算之後讓 CC 的某一行為 0 (CC 不可逆)，代表某些狀態是其他狀態的組合。把這些不獨立的狀態都代換掉之後，重新新整理微分方程或者如果可以做某些行運算(等式兩邊右乘矩陣是做行運算，等式兩邊左乘矩陣是做列運算)之後讓 CC 變成單位矩陣，產生一個新的 AA 和 BB 的微分方程：

dx tdt=x tA+e i(ωt+p)B\frac{d x_t}{d t} = x_t A + e^{i (\omega t + p)} B

以 x t=e i(ωt+p)y tx_t = e^{i (\omega t + p)} y_t 做變數變換，只專注去掉 e i(ωt+p)e^{i (\omega t + p)} 的部分表達的狀態，則：

iωe i(ωt+p)y t+e i(ωt+p)dy tdt=dx tdt=x tA+e i(ωt+p)B=e i(ωt+p)y tA+e i(ωt+p)Bi \omega e^{i(\omega t + p)} y_t + e^{i(\omega t + p)}\frac{d y_t}{d t} = \frac{d x_t}{d t} = x_t A + e^{i(\omega t + p)} B = e^{i(\omega t + p)} y_t A + e^{i(\omega t + p)} B

原 x tx_t 微分方程式就變成 y ty_t 的常微分方程式：

dy tdt=y t(A−iωI)+B\frac{d y_t}{d t} = y_t ( A - i \omega I ) + B

所以(參見 數學線性微分方程知識 中提到的數學)它的解是：

y t=tBβ(t(A−iωI))+y 0α(t(A−iωI))y_t = t B \beta\left(t ( A - i \omega I )\right) + y_0 \alpha\left(t ( A - i \omega I )\right)

所以

x t=e i(ωt+p)(tBβ(t(A−iωI))+y 0α(t(A−iωI)))=e i(ωt+p)tBβ(t(A−iωI))+e iωtx 0α(t(A−iωI))x_t = e^{i(\omega t + p)} \left( t B \beta\left(t ( A - i \omega I )\right) + y_0 \alpha\left(t ( A - i \omega I )\right) \right)= e^{i(\omega t + p)} t B \beta \left(t (A - i \omega I)\right) + e^{i\omega t} x_0 \alpha\left(t (A - i \omega I)\right)

程式可以畫出隨著時間進展的 x tx_t 或 y ty_t ，(如果 α(t(A−iωI))\alpha ( t ( A - i \omega I )) 最後趨近 0) 最後穩定狀態以 yy 表達是 y=−B(A−iωI) −1y = - B ( A - i \omega I )^{-1} ，以 xx 表達是 x=−e i(ωt+p)B(A−iωI) −1x = - e^{i(\omega t + p)} B \left( A - i \omega I\right)^{-1} ，對應的實部就是各迴路的電壓或電流數值。

例一

RCL電路，QQ 是電容器的電量， 1CQ\frac{1}{C} Q 的電容器的電壓， dQdt\frac{d Q}{d t} 是電流， RdQdtR \frac{d Q}{d t} 是電阻的電壓， d 2Qdt 2\frac{d^2 Q}{d t^2} 是電流的微分， Ld 2Qdt 2L \frac{d^2 Q}{d t^2} 是電感器的電壓，vv 是交流電源電壓最大值：

1CQ+RdQdt+Ld 2Qdt 2=vcos(ωt+p)\frac{1}{C} Q + R \frac{d Q}{d t} + L \frac{d^2 Q}{d t^2} = v \cos(\omega t + p)

寫成矩陣：

cos(ωt+p)[v 0]=[Q I dIdt dQdt][1C 0 R 1 L 0 0 −1]=[dIdt dQdt][L 0 0 −1]+[I Q][R 1 1C 0] [dIdt dQdt][L 0 0 −1]=[I Q][−R −1 −1C 0]+[vcos(ωt+p) 0] [dIdt dQdt]=[I Q][−RL −1 −1LC 0]+cos(ωt+p)[vL 0]\begin{array}{l}\cos(\omega t + p) \begin{bmatrix}v&0\end{bmatrix} = \begin{bmatrix}Q&I&\frac{d I}{d t}&\frac{d Q}{d t}\end{bmatrix} \begin{bmatrix}\frac{1}{C}&0\\R&1\\L&0\\0&-1\end{bmatrix}= \begin{bmatrix}\frac{d I}{d t}&\frac{d Q}{d t}\end{bmatrix} \begin{bmatrix}L&0\\0&-1\end{bmatrix} + \begin{bmatrix}I&Q\end{bmatrix} \begin{bmatrix}R&1\\\frac{1}{C}&0\end{bmatrix}\\\begin{bmatrix}\frac{d I}{d t}&\frac{d Q}{d t}\end{bmatrix} \begin{bmatrix}L&0\\0&-1\end{bmatrix} = \begin{bmatrix}I&Q\end{bmatrix} \begin{bmatrix}-R&-1\\-\frac{1}{C}&0\end{bmatrix} + \begin{bmatrix}v \cos(\omega t + p)&0\end{bmatrix}\\\begin{bmatrix}\frac{d I}{d t}&\frac{d Q}{d t}\end{bmatrix}= \begin{bmatrix}I&Q\end{bmatrix}\begin{bmatrix}-\frac{R}{L}&-1\\-\frac{1}{L C}&0\end{bmatrix} + \cos(\omega t + p) \begin{bmatrix}\frac{v}{L}&0\end{bmatrix}\end{array}

長的是這個樣子 dx tdt=x tA+e i(ωt+p)B\frac{d x_t}{d t} = x_t A + e^{i(\omega t + p)} B

與使用複數表示阻抗的關係

接續例一的 RCL電路，它的 y ty_t 微分方程式是：

[dy Idt dy Qdt]=[y I y Q][−RL−iω 1 −1LC −iω]+[vL 0]\begin{bmatrix}\frac{d y_I}{d t}&\frac{d y_Q}{d t}\end{bmatrix} = \begin{bmatrix}y_I&y_Q\end{bmatrix} \begin{bmatrix}-\frac{R}{L} - i \omega&1\\-\frac{1}{L C}&-i \omega\end{bmatrix} + \begin{bmatrix}\frac{v}{L}&0\end{bmatrix}

最後穩定狀態是：

y=−[vL 0][−RL−iω 1 −1LC −iω] −1y = -\begin{bmatrix}\frac{v}{L}&0\end{bmatrix} \begin{bmatrix}-\frac{R}{L} - i \omega&1\\-\frac{1}{L C}&-i \omega\end{bmatrix}^{-1}

如果進一步簡化狀態變數，專注在電流，把牽涉電感的狀態變數除以 iωi \omega，牽涉電容電量的狀態變數乘以 iωi \omega ，則這時候電流狀態變數對應的矩陣的數值就是用複數表示的阻抗。定義 zz 狀態：

z I≡y I z Q≡iωy Q [dz Idt dz Qdt]=[dy Idt dy Qdt][1 0 0 iω]=([z I z Q][1 0 0 1iω][−RL−iω 1 −1LC −iω]+[vL 0])[1 0 0 iω] =[z I z Q][−RL−iω iω −1iωLC −iω]+[vL 0]\begin{array}{l}z_I \equiv y_I\\z_Q \equiv i \omega y_Q\\\begin{bmatrix}\frac{d z_I}{d t}&\frac{d z_Q}{d t}\end{bmatrix} = \begin{bmatrix}\frac{d y_I}{d t}&\frac{d y_Q}{d t}\end{bmatrix} \begin{bmatrix}1&0\\0&i \omega\end{bmatrix} = \left( \begin{bmatrix}z_I&z_Q\end{bmatrix} \begin{bmatrix}1&0\\0&\frac{1}{i \omega}\end{bmatrix} \begin{bmatrix}-\frac{R}{L} - i \omega &1\\-\frac{1}{L C}&-i \omega\end{bmatrix} + \begin{bmatrix}\frac{v}{L}&0\end{bmatrix}\right) \begin{bmatrix}1&0\\0&i \omega\end{bmatrix} \\= \begin{bmatrix}z_I&z_Q\end{bmatrix} \begin{bmatrix}-\frac{R}{L} - i \omega &i \omega\\-\frac{1}{i \omega L C}&-i \omega\end{bmatrix} + \begin{bmatrix}\frac{v}{L}&0\end{bmatrix}\end{array}

變成 z tz_t 的常微分方程式。穩定狀態是：

0=[z I z Q][−RL−iω iω −1iωLC −iω]+[vL 0]0 = \begin{bmatrix}z_I&z_Q\end{bmatrix} \begin{bmatrix}-\frac{R}{L} - i \omega &i \omega\\-\frac{1}{i \omega L C}&-i \omega\end{bmatrix} + \begin{bmatrix}\frac{v}{L}&0\end{bmatrix}

因為 0=[z I z Q][iω −iω]0 = \begin{bmatrix}z_I&z_Q\end{bmatrix} \begin{bmatrix}i \omega\\ -i \omega\end{bmatrix} ，此時同一個電流的相關 zz 狀態值都一樣；

0=z I[1 1][−R−iωL −1iωC]+v=z I(−R−iωL−1iωC)+v0 = z_I \begin{bmatrix}1&1\end{bmatrix} \begin{bmatrix}-R - i \omega L\\-\frac{1}{i \omega C}\end{bmatrix} + v = z_I \left( - R - i \omega L - \frac{1}{i \omega C} \right) + v

所以，

z I(R+iωL+1iωC)=vz_I \left( R + i \omega L + \frac{1}{i \omega C} \right) = v

如果只對最終穩定狀態感興趣，可以用 zz 狀態去直接寫聯立線性方程式，此時因為電流的任一階積分或任一階微分的量 (電容器是電流的的一階積分電子元件，電感器是電流的一階微分電子元件，目前市面上並沒有電流其他階積分或微分的電子元件) 都以同一個狀態數值表示，矩陣的大小會變小，假設這個電路有 s 個迴路，變成解 zA=bz A = b 的線性聯立方程式問題。其中 AA 為 s 乘 s 矩陣，zz 和 bb 為 1 乘 s 矩陣，AA 的組成是以複數表示的阻抗，bb 的組成是除掉 e i(ωt+p)e^{i(\omega t + p)} 之後複數表示的電壓。AA 矩陣會是對稱矩陣；一個電阻是 RR 歐姆，每個迴路看到的電阻都是 RR 歐姆，一個電容器是 CC 法拉，每個迴路看到的電容都是 CC 法拉。要特別注意的是多隻腳的電感器。迴路 1 有一個電感器電感值是 L 1L_1 亨利，迴路 2 有一個電感器電感值是 L 2L_2 亨利，如果這兩個電感器有共用線圈或是共用磁場鐵棒，則在沿迴路 1 寫電壓的時候，迴路 2 電流對迴路 1 貢獻的電壓數字的電感係數不是 L 2L_2 ，而是 MM，稱之為感應電感，理論數值為 L 1L 2\sqrt{L_1 L_2} 亨利。電感數值和線線圈個數的平方成正比，通常線圈個數也和電感器的長度成正比 (電感器的製作方法是絕緣漆銅線纏繞著一個鐵棒，所以鐵棒長度和線圈數成正比)，所以電感數值和長度的平方成正比。當這兩個電感器只有兩隻腳，不同迴路看到的電感都是 LL 所以感應電感 LL\sqrt{L L} 還是 LL，情況就變得像電阻或電容一樣；換個說法，在計算一個迴路的電壓的時候，另一個迴路的電流在電阻或電容或只有兩隻腳的電感貢獻的電壓和原本的電阻或電容或電感一樣，多隻腳的電感器 (或是電路板因為 layout 不良，距離太靠近的兩個兩隻腳電感線圈) 因為磁場互相影響的緣故情況比較特別，另一個迴路的電流在這個多腳電感器貢獻的電壓是用電感理論值 L 1L 2\sqrt{L_1 L_2} 來計算。

例二

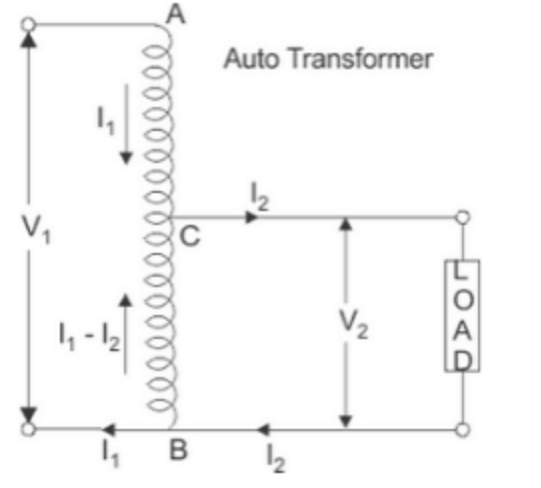
這邊有二個迴路，迴路 1 的電流是 I 1I_1 迴路 2 的電流是 I 2I_2 ，這個三隻腳電感器在迴路 1 ( AB ) 是 LL 亨利，在迴路 2 的電感器( CB ) 長度只有一半是 L4\frac{L}{4} 亨利，所以 M=LL4=L2M = \sqrt{L \frac{L}{4}} = \frac{L}{2} ，LOAD 是個電暖爐電阻是 RR。此時迴路 1 和迴路 2 的壓降數學式不是：

0=V 1−LdI 1dt+L4dI 2dt 0=L4dI 1dt−L4dI 2dt−RI 2\begin{array}{l}0 = V_1 - L \frac{d I_1}{d t} + \frac{L}{4} \frac{d I_2}{d t}\\0 = \frac{L}{4} \frac{d I_1}{d t} - \frac{L}{4} \frac{d I_2}{d t} - R I_2\end{array}

而是：

0=V 1−LdI 1dt+L2dI 2dt 0=L2dI 1dt−L4dI 2dt−RI 2\begin{array}{l}0 = V_1 - L \frac{d I_1}{d t} + \frac{L}{2} \frac{d I_2}{d t}\\0 = \frac{L}{2} \frac{d I_1}{d t} - \frac{L}{4} \frac{d I_2}{d t} - R I_2\end{array}

直接寫成 zz 方程式，設最終解 I 1=z 1e i(ωt+p),I 2=z 2e i(ωt+p)I_1 = z_1 e^{i(\omega t + p)},I_2 = z_2 e^{i(\omega t + p)} ：

[v 0]=[z 1 z 2][iωL iωL2 −iωL2 −iωL4−R]\begin{bmatrix}v&0\end{bmatrix} = \begin{bmatrix}z_1&z_2\end{bmatrix} \begin{bmatrix}i \omega L&\frac{i \omega L}{2}\\- \frac{i \omega L}{2}&- \frac{i \omega L}{4} - R\end{bmatrix}

所以

[z 1 z 2]=[v4R+viωL v2R]\begin{bmatrix}z_1&z_2\end{bmatrix} = \begin{bmatrix}\frac{v}{4 R} + \frac{v}{i \omega L}&\frac{v}{2 R}\end{bmatrix}

要知道到底電流如何隨著時間穩定到最終的週期電流：

0 =[dI 1dt dI 2dt I 1 I 2][−L L2 L2 −L4 0 0 0 −R]+[vcos(ωt+p) 0] =[dI 1dt dI 2dt][−L L2 L2 −L4]+[I 1 I 2][0 0 0 −R]+[vcos(ωt+p) 0] [dI 1dt dI 2dt][L −L2 −L2 L4] =[I 1 I 2][0 0 0 −R]+[vcos(ωt+p) 0]\begin{aligned}0 &= \begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}&I_1&I_2\end{bmatrix} \begin{bmatrix}-L&\frac{L}{2}\\\frac{L}{2}&-\frac{L}{4}\\0&0\\0&-R\end{bmatrix} + \begin{bmatrix}v \cos(\omega t + p)&0\end{bmatrix}\\&= \begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}-L&\frac{L}{2}\\\frac{L}{2}&-\frac{L}{4}\end{bmatrix} + \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}0&0\\0&-R\end{bmatrix} + \begin{bmatrix}v \cos(\omega t + p)&0\end{bmatrix}\\\begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}L&-\frac{L}{2}\\-\frac{L}{2}&\frac{L}{4}\end{bmatrix} &= \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}0&0\\0&-R\end{bmatrix} + \begin{bmatrix}v \cos(\omega t + p)&0\end{bmatrix}\end{aligned}

擴展到複數表示：

[dI 1dt dI 2dt][L −L2 −L2 L4]=[I 1 I 2][0 0 0 −R]+e i(ωt+p)[v 0]\begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}L&-\frac{L}{2}\\-\frac{L}{2}&\frac{L}{4}\end{bmatrix} = \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}0&0\\0&-R\end{bmatrix} + e^{i(\omega t + p)}\begin{bmatrix}v&0\end{bmatrix}

注意到 [L −L2 −L2 L4]\begin{bmatrix}L&-\frac{L}{2}\\-\frac{L}{2}&\frac{L}{4}\end{bmatrix} 不可逆：

[dI 1dt dI 2dt][L 0 −L2 0]=[I 1 I 2][0 0 0 −R]+e i(ωt+p)[v v2]\begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}L&0\\-\frac{L}{2}&0\end{bmatrix} = \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}0&0\\0&-R\end{bmatrix} + e^{i(\omega t + p)}\begin{bmatrix}v&\frac{v}{2}\end{bmatrix} array I 2I_2 只能是 v2Re i(ωt+p)\frac{v}{2 R} e^{i(\omega t + p)} 不能亂選，原本微分方程式在代換之後變成：

LdI 1dt−L2iωv2Re i(ωt+p)=ve i(ωt+p)L \frac{d I_1}{d t}-\frac{L}{2}\frac{i \omega v}{2R}e^{i(\omega t+p)}=v e^{i(\omega t+p)}

也就是：

dI 1dt=e i(ωt+p)(vL+iωv4R)\frac{d I_1}{d t} = e^{i(\omega t + p)} \left(\frac{v}{L} + \frac{i \omega v}{4 R} \right)

由上面提過的一般解：

I 1t =e i(ωt+p)t(vL+iωv4R)β(−iωt)+e iωtx 0α(−iωt)=e i(ωt+p)t(vL+iωv4R)e −iωt−1−iωt+e iωtx 0e −iωt =(viωL+v4R)e i(ωt+p)−(viωL+v4R)e ip+x 0\begin{aligned}I_{1t} &= e^{i(\omega t + p)} t \left( \frac{v}{L} + \frac{i \omega v}{4 R} \right)\beta(-i \omega t) + e^{i\omega t} x_0 \alpha(-i \omega t) = e^{i(\omega t + p)} t \left( \frac{v}{L} + \frac{i \omega v}{4 R} \right) \frac{e^{-i \omega t} - 1}{- i \omega t} + e^{i \omega t} x_0 e^{- i \omega t}\\&= \left( \frac{v}{i \omega L} + \frac{v}{4 R} \right) e^{i(\omega t + p)} - \left( \frac{v}{i \omega L} + \frac{v}{4 R} \right) e^{i p} + x_0\end{aligned}

這裡 (viωL+v4R)e i(ωt+p)\left( \frac{v}{i \omega L} + \frac{v}{4 R} \right) e^{i(\omega t + p)} 是上面找到的最終解，但是 α(t(A−iω)I)\alpha(t(A - i \omega) I) 在這個例子並沒有趨近 0 ，所以說這句話 "設最終解 I 1=z 1e i(ωt+p),I 2=z 2e i(ωt+p)I_1 = z_1 e^{i(\omega t + p)}, I_2 = z_2 e^{i(\omega t + p)}" 或類似的話的時候邏輯上要小心。其實在這個例子裡從最原始微分方程就可以看到數學上 I 1tI_{1 t} 加上任何常數都還是解。 其實因為實際的電路總是有小小的電阻，所以最終來自初始值 x 0x_0 的貢獻都會隨著時間逐漸消失，這也是直接求最終解是實際上合理的原因。

功率

電壓乘電流就是功率瓦數也就是每秒鐘花掉的焦耳數。當電壓和電流符號相反的時候這個數字是負的，意思是還回去電源的功率。直流電的時候，零功率必定表示沒有電壓或沒有電流，所以沒有提供任何能量殺不了人。交流電的時候，因為電壓和電流時時刻刻在變，所以一般家電用品標示的功率是平均功率的概念，因此 0 平均功率可能還是會殺人，因為某個瞬間的功率會是很大的數字。

假設電壓是 Vcos(ωt)V \cos(\omega t) ，電流是 Icos(ωt+p)I \cos(\omega t + p) ，之間的相位角度相差 pp ，則在時刻 tt 的瞬間功率是 Vcos(ωt)Icos(ωt+p)=VI2(cos(p)+cos(2ωt+p))V \cos(\omega t) I \cos(\omega t + p) = \frac{V I}{2} (\cos(p) + \cos(2 \omega t + p))，這個瞬間功率介於 VI2(cos(p)−1)\frac{V I}{2} (\cos(p)-1) 和 VI2(cos(p)+1)\frac{V I}{2} (\cos(p)+1) 之間，積分一個周期再除以一個週期得到的平均功率是 VI2cos(p)\frac{V I}{2} \cos(p) 。負載複數就是電壓複數乘以電流複數，當負載複數沒有虛部的時候，電壓複數和電流複數之間的角度 p=0p = 0 或是 p=πp = \pi 。雖然電壓或電流各自都很大，但是當電壓電流角度相差 90 度的時候平均功率是 0。交流電的時候所謂的平均電壓或平均電流也是一個週期平均的概念，但是如果只是原本數字的平均因為一直在 0 上下震盪所以是零，所以平均的定義是平方的平均再取平方根；積分 (Vcos(ωt)) 2( V \cos(\omega t ))^2 和 (Icos(ωt+p)) 2(I \cos(\omega t + p ))^2 一個周期再除以一個週期再取平方根是 V2\frac{V}{\sqrt{2}} 和 I2\frac{I}{\sqrt{2}} ，三用電表測量的 rms 交流電壓數字就是這個數字，於是平均功率就成為是平均電壓乘上平均電流再乘上 cos(p)\cos(p) 。平均交流電壓或電流沒有負的數字，有時候圖上故意寫上負號是為了表達角度相差 180 度。所以口語說交流電壓 120 伏特，其實瞬間電壓可以有 1202120\sqrt{2} 伏特或 −1202-120\sqrt{2} 伏特，這是在示波器上可以看的波浪圖形的最高點或最低點。同樣是 40 安培的保險絲，交流電保險絲也比直流電保險絲強壯，把交流電保險絲拿來當直流電保險絲用，該燒斷的時候可能沒燒斷。一個交流電家電消耗的平均功率不大，但是瞬間功率和瞬間電流可以很大。

例三

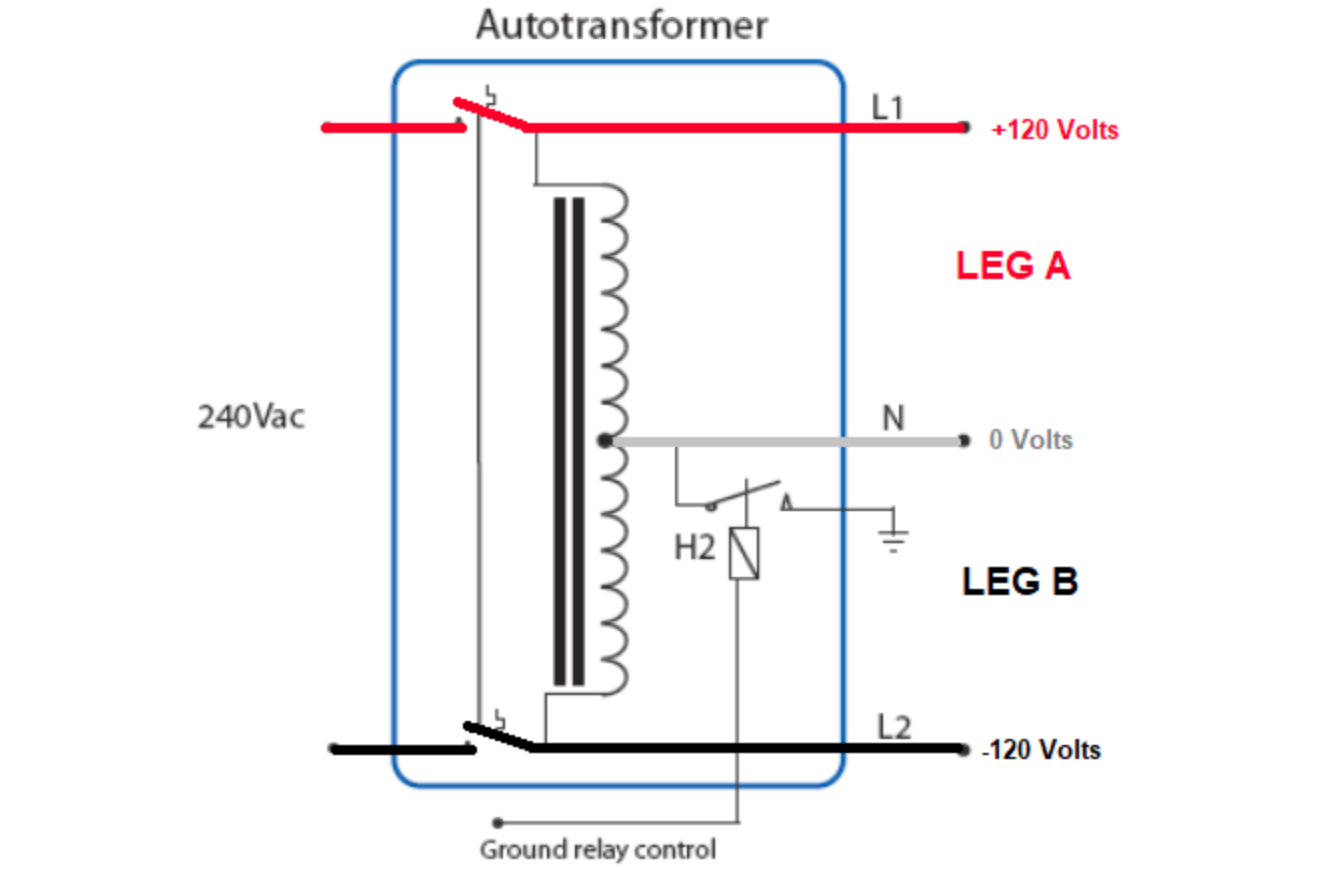
總共四個迴路，線路 0 是一個 240 伏特交流電壓源 V 0=vcos(ωt+p)V_0 = v \cos(\omega t + p) 和有三隻腳的主線圈導引出二個 120 伏特電源，迴路 0 和迴路 1 和迴路 2 共用電感器的鐵棒，迴路 1 和迴路 2 是二個導引出的 120 伏特各自接上負載，迴路 3 是 240 伏特電壓源直接接上負載提供給需要 240 伏特的電器，整條線圈導線有小小的電阻 rr 。電阻值和導線長度成正比，不像電感。四個迴路的壓降方程式是：

0 =V 0−rI 0−LdI 0dt+r2I 1+L2dI 1dt+r2I 2+L2dI 2dt 0 =r2I 0+L2dI 0dt−r2I 1−L4dI 1dt−L4dI 2dt−(LOAD 1:a formula of I 1 and its integration or derivative of any order) 0 =r2I 0+L2dI 0dt−L4dI 1dt−r2I 2−L4dI 2dt−(LOAD 2:a formula of I 2 and its integration or derivative of any order) 0 =V 0−(LOAD 3:a formula of I 3 and its integration or derivative of any order)\begin{aligned}0 &= V_0 - r I_0 - L \frac{d I_0}{d t} + \frac{r}{2} I_1 + \frac{L}{2} \frac{d I_1}{d t} + \frac{r}{2} I_2 + \frac{L}{2} \frac{d I_2}{d t}\\0 &= \frac{r}{2} I_0 + \frac{L}{2} \frac{d I_0}{d t} - \frac{r}{2} I_1 - \frac{L}{4} \frac{d I_1}{d t} - \frac{L}{4} \frac{d I_2}{d t} - (LOAD_1: \text{a formula of }I_1\text{ and its integration or derivative of any order})\\0 &= \frac{r}{2} I_0 + \frac{L}{2} \frac{d I_0}{d t} - \frac{L}{4} \frac{d I_1}{d t} - \frac{r}{2} I_2 - \frac{L}{4} \frac{d I_2}{d t} - (LOAD_2 : \text{a formula of }I_2\text{ and its integration or derivative of any order} )\\0 &= V_0 - (LOAD_3 : \text{a formula of }I_3\text{ and its integration or derivative of any order} )\end{aligned}

例如如果 LOADLOAD 只是電阻：

0=[dI 0dt dI 1dt dI 2dt dI 3dt][−L L2 L2 0 L2 −L4 −L4 0 L2 −L4 −L4 0 0 0 0 0]+[I 0 I 1 I 2 I 3][−r r2 r2 0 r2 −R 1−r2 0 0 r2 0 −R 2−r2 0 0 0 0 −R 3]+e i(ωt+p)[v 0 0 v] [dI 0dt dI 1dt dI 2dt dI 3dt][L −L2 −L2 0 −L2 L4 L4 0 −L2 L4 L4 0 0 0 0 0]=[I 0 I 1 I 2 I 3][−r r2 r2 0 r2 −R 1−r2 0 0 r2 0 −R 2−r2 0 0 0 0 −R 3]+e i(ωt+p)[v 0 0 v]\begin{aligned}0 = \begin{bmatrix}\frac{d I_0}{d t}&\frac{d I_1}{d t}&\frac{d I_2}{d t}&\frac{d I_3}{d t}\end{bmatrix} \begin{bmatrix}-L&\frac{L}{2}&\frac{L}{2}&0\\\frac{L}{2}&-\frac{L}{4}&-\frac{L}{4}&0\\\frac{L}{2}&-\frac{L}{4}&-\frac{L}{4}&0\\0&0&0&0\end{bmatrix} + \begin{bmatrix}I_0&I_1&I_2&I_3\end{bmatrix} \begin{bmatrix}-r&\frac{r}{2}&\frac{r}{2}&0\\\frac{r}{2}&-R_1- \frac{r}{2}&0&0\\\frac{r}{2}&0&-R_2-\frac{r}{2}&0\\0&0&0&-R_3\end{bmatrix} + e^{i(\omega t + p)} \begin{bmatrix}v&0&0&v\end{bmatrix}\\\begin{bmatrix}\frac{d I_0}{d t}&\frac{d I_1}{d t}&\frac{d I_2}{d t}&\frac{d I_3}{d t}\end{bmatrix} \begin{bmatrix}L&-\frac{L}{2}&-\frac{L}{2}&0\\-\frac{L}{2}&\frac{L}{4}&\frac{L}{4}&0\\-\frac{L}{2}&\frac{L}{4}&\frac{L}{4}&0\\0&0&0&0\end{bmatrix}= \begin{bmatrix}I_0&I_1&I_2&I_3\end{bmatrix} \begin{bmatrix}-r&\frac{r}{2}&\frac{r}{2}&0\\\frac{r}{2}&-R_1- \frac{r}{2}&0&0\\\frac{r}{2}&0&-R_2-\frac{r}{2}&0\\0&0&0&-R_3\end{bmatrix} + e^{i(\omega t + p)} \begin{bmatrix}v&0&0&v\end{bmatrix}\end{aligned}

I 3I_3 沒得選， I 3=vR 3e i(ωt+p)I_3 = \frac{v}{R_3} e^{i(\omega t + p)} 。行運算，第一行乘上 12\frac{1}{2} 加到第二和第三行：

[dI 0dt dI 1dt dI 2dt][L 0 0 −L2 0 0 −L2 0 0]=[I 0 I 1 I 2][−r 0 0 r2 −R 1−r4 r4 r2 r4 −R 2−r4]+e i(ωt+p)[v v2 v2]\begin{bmatrix}\frac{d I_0}{d t}&\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}L&0&0\\-\frac{L}{2}&0&0\\-\frac{L}{2}&0&0\end{bmatrix} = \begin{bmatrix}I_0&I_1&I_2\end{bmatrix} \begin{bmatrix}-r&0&0\\\frac{r}{2}&-R_1 - \frac{r}{4}&\frac{r}{4}\\\frac{r}{2}&\frac{r}{4}&-R_2 - \frac{r}{4}\end{bmatrix} + e^{i(\omega t + p)} \begin{bmatrix}v&\frac{v}{2}&\frac{v}{2}\end{bmatrix}

所以

[dI 0dt dI 1dt dI 2dt][L −L2 −L2]=[I 0 I 1 I 2][−r r2 r2]+e i(ωt+p)v 0=[I 0 I 1 I 2][0 0 −R 1−r4 r4 r4 −R 2−r4]+e i(ωt+p)[v2 v2]=[I 1 I 2][−R 1−r4 r4 r4 −R 2−r4]+e i(ωt+p)[v2 v2]\begin{aligned}\begin{bmatrix}\frac{d I_0}{d t}&\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}L\\-\frac{L}{2}\\-\frac{L}{2}\end{bmatrix} = \begin{bmatrix}I_0&I_1&I_2\end{bmatrix} \begin{bmatrix}-r\\\frac{r}{2}\\\frac{r}{2}\end{bmatrix} + e^{i(\omega t + p)} v\\0 = \begin{bmatrix}I_0&I_1&I_2\end{bmatrix} \begin{bmatrix}0&0\\-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix} + e^{i(\omega t + p)} \begin{bmatrix}\frac{v}{2}&\frac{v}{2}\end{bmatrix} = \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix} + e^{i(\omega t + p)} \begin{bmatrix}\frac{v}{2}&\frac{v}{2}\end{bmatrix}\end{aligned}

I 1I_1 和 I 2I_2 被決定：

[I 1 I 2]=−e i(ωt+p)[v2 v2][−R 1−r4 r4 r4 −R 2−r4] −1\begin{bmatrix}I_1&I_2\end{bmatrix}= -e^{i(\omega t + p)} \begin{bmatrix}\frac{v}{2}&\frac{v}{2}\end{bmatrix} \begin{bmatrix}-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix}^{-1}

I 0I_0 方程式：

LdI 0dt+[dI 1dt dI 2dt][−L2 −L2]=−rI 0+[I 1 I 2][r2 r2]+e i(ωt+p)v LdI 0dt+iωe i(ωt+p)[v2 v2][−R 1−r4 r4 r4 −R 2−r4] −1[L2 L2]=−rI 0−e i(ωt+p)[v2 v2][−R 1−r4 r4 r4 −R 2−r4] −1[r2 r2]+e i(ωt+p)v LdI 0dt=−rI 0+e i(ωt+p)(v−(rv4+iωLv4)[1 1][−R 1−r4 r4 r4 −R 2−r4] −1[1 1])\begin{aligned}L \frac{d I_0}{d t} + \begin{bmatrix}\frac{d I_1}{d t}&\frac{d I_2}{d t}\end{bmatrix} \begin{bmatrix}-\frac{L}{2}\\-\frac{L}{2}\end{bmatrix} = - r I_0 + \begin{bmatrix}I_1&I_2\end{bmatrix} \begin{bmatrix}\frac{r}{2}\\\frac{r}{2}\end{bmatrix} + e^{i(\omega t + p)} v\\L \frac{d I_0}{d t} + i \omega e^{i(\omega t + p)} \begin{bmatrix}\frac{v}{2}&\frac{v}{2}\end{bmatrix} \begin{bmatrix}-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix}^{-1} \begin{bmatrix}\frac{L}{2}\\\frac{L}{2}\end{bmatrix} = - r I_0 - e^{i(\omega t + p)} \begin{bmatrix}\frac{v}{2}&\frac{v}{2}\end{bmatrix} \begin{bmatrix}-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix}^{-1}\begin{bmatrix}\frac{r}{2}\\\frac{r}{2}\end{bmatrix} + e^{i(\omega t + p)} v\\L \frac{d I_0}{d t} = - r I_0 + e^{i(\omega t + p)} \left( v - \left(\frac{r v}{4} + \frac{i \omega L v}{4}\right) \begin{bmatrix}1&1\end{bmatrix} \begin{bmatrix}-R_1-\frac{r}{4}&\frac{r}{4}\\\frac{r}{4}&-R_2-\frac{r}{4}\end{bmatrix}^{-1} \begin{bmatrix}1\\1\end{bmatrix}\right)\end{aligned}

還是長這個樣子 dx tdt=x tA+e i(ωt+p)B\frac{d x_t}{d t} = x_t A + e^{i(\omega t + p)} B

直接找最終狀態。設最終解 I 0=z 0e i(ωt+p),I 1=z 1e i(ωt+p),I 2=z 2e i(ωt+p),I 3=z 3e i(ωt+p)I_0 = z_0 e^{i(\omega t + p)},I_1 = z_1 e^{i(\omega t + p)},I_2 = z_2 e^{i(\omega t + p)},I_3 = z_3 e^{i(\omega t + p)} ，對應的 zz 方程式是：

[v 0 0 v]=[z 0 z 1 z 2 z 3][r+iωL −r2−iωL2 −r2−iωL2 0 −r2−iωL2 LOAD 1+r2+iωL4 iωL4 0 −r2−iωL2 iωL4 LOAD 2+r2+iωL4 0 0 0 0 LOAD 3]\begin{bmatrix}v&0&0&v\end{bmatrix} = \begin{bmatrix}z_0&z_1&z_2&z_3\end{bmatrix} \begin{bmatrix}r + i \omega L&- \frac{r}{2} - \frac{i \omega L}{2}&-\frac{r}{2} - \frac{i \omega L}{2}&0\\-\frac{r}{2} - \frac{i \omega L}{2}&LOAD_1 + \frac{r}{2} + \frac{i \omega L}{4}&\frac{i \omega L}{4}&0\\-\frac{r}{2} - \frac{i \omega L}{2}&\frac{i \omega L}{4}&LOAD_2 + \frac{r}{2} + \frac{i \omega L}{4}&0\\0&0&0&LOAD_3\end{bmatrix}

解出來(藉由 Mathematica™ 幫忙)是：

z 0 =r(iωL+r)+LOAD 1(iωL+2r)+LOAD 2(iωL+2r)+4LOAD 1LOAD 2(iωL+r)(rLOAD 1+rLOAD 2+4LOAD 1LOAD 2)v z 1 =r+2LOAD 2rLOAD 1+rLOAD 2+4LOAD 1LOAD 2v z 2 =r+2LOAD 1rLOAD 1+rLOAD 2+4LOAD 1LOAD 2v z 3 =1LOAD 3v\begin{aligned}z_0 &= \frac{r (i \omega L + r) + LOAD_1 (i \omega L + 2 r) + LOAD_2 (i \omega L + 2 r) + 4 LOAD_1 LOAD_2}{( i \omega L + r ) ( r LOAD_1 + r LOAD_2 + 4 LOAD_1 LOAD_2)}v\\z_1 &= \frac{r + 2 LOAD_2}{r LOAD_1 + r LOAD_2 + 4 LOAD_1 LOAD_2}v\\z_2 &= \frac{r + 2 LOAD_1}{r LOAD_1 + r LOAD_2 + 4 LOAD_1 LOAD_2}v\\z_3 &= \frac{1}{LOAD_3} v\end{aligned}

總電流是 z 0+z 3z_0 + z_3 把這個數值寫成 vke iθv k e^{i \theta} ，總瓦數是 12v 2kcos(θ)\frac{1}{2} v^2 k \cos(\theta) 。當沒接上負載的時候，等同於 LOAD 1LOAD_1 和 LOAD 2LOAD_2 和 LOAD 3LOAD_3 是無限大，這時候 z 0=viωL+r,z 1=z 2=z 3=0z_0 = \frac{v}{i \omega L + r},z_1 = z_2 = z_3 = 0 。如果線圈電阻幾乎是零則 θ\theta 幾乎是90度，kk 幾乎是 1ωL\frac{1}{\omega L} 。

或者使用 gnu scientific library 程式庫和 C 語言內建的複數計算功能，以下這個程式是解這個電路： 

#include <stdio.h>  
#include <complex.h>  
#include <gsl/gsl_complex.h>  
#include <gsl/gsl_complex_math.h>  
#include <gsl/gsl_linalg.h>
 
#define LOOP_NUM 4
 
void currentSum(char* la, gsl_complex xx) {  
printf("%s: %f%+fI size %f theta %f\n", la, crealf(xx), cimagf(xx), gsl_complex_abs(xx) / M_SQRT2, gsl_complex_arg(xx));  
}
 
void loopData(char* la, gsl_complex voltage, gsl_complex current) {  
double the = gsl_complex_arg(current) - gsl_complex_arg(voltage);  
double vs = gsl_complex_abs(voltage) / M_SQRT2;  
double is = gsl_complex_abs(current) / M_SQRT2;  
printf("%s: voltage %f%+fI size %f current %f%+fI size %f theta %f watt %f\n", la, crealf(voltage), cimagf(voltage), vs, crealf(current), cimagf(current), is, the, vs * is * cos(the));  
}
 
int main(void) {  
gsl_complex iw = 2 * M_PI * 60 * I;  
gsl_complex v = 240 * M_SQRT2 * gsl_complex_exp(I * 0);  
gsl_complex load1 = 1.0e+1 + 1.1e+0 * I;  
gsl_complex load2 = 2.0e+1 - 1.2e+2 * I;  
gsl_complex load3 = 8.0e-1 + 1.3e+1 * I;  
double coil_R = 1.0e-2;  
double coil_L = 1.945;
 
/* only upper triangle and diagonal are used for saving keystrokes labor */  
gsl_complex a_data[] = {  
coil_R + coil_L * iw, -coil_R /2 -coil_L /2 * iw, -coil_R/2 -coil_L /2 * iw, 0,  
0, load1 + coil_R /2 + coil_L /4 * iw, coil_L /4 * iw, 0,  
0, 0, load2 + coil_R/2 + coil_L /4 * iw, 0,  
0, 0, 0, load3  
};  
int i, j;  
for (i=0; i\<LOOP_NUM; i++) {  
for (j=i+1; j\<LOOP_NUM; j++) {  
a_data[LOOP_NUM * j +i] = a_data[LOOP_NUM * i +j];  
}  
}  
/* solve A x = b */  
gsl_matrix_complex_view A = gsl_matrix_complex_view_array(a_data, LOOP_NUM, LOOP_NUM);  
gsl_complex b_data[] = { v, 0, 0, v };  
gsl_vector_complex_view b = gsl_vector_complex_view_array(b_data, LOOP_NUM);  
gsl_vector_complex *x = gsl_vector_complex_alloc (LOOP_NUM);
 
int s;  
gsl_permutation * p = gsl_permutation_alloc (LOOP_NUM);  
gsl_linalg_complex_LU_decomp (&A.matrix, p, &s);  
if ((s=gsl_linalg_complex_LU_solve (&A.matrix, p, &b.vector, x)) ) {  
printf("weird! not invertible %d\n", s);  
exit -1;  
}  
/* show result */  
currentSum("I0+I3", GSL_VECTOR_COMPLEX(x, 0)+GSL_VECTOR_COMPLEX(x, 3));  
currentSum("I0-I1", GSL_VECTOR_COMPLEX(x, 0)-GSL_VECTOR_COMPLEX(x, 1));  
currentSum("I0-I2", GSL_VECTOR_COMPLEX(x, 0)-GSL_VECTOR_COMPLEX(x, 2));  
currentSum("I1-I2", GSL_VECTOR_COMPLEX(x, 1)-GSL_VECTOR_COMPLEX(x, 2));  
loopData("source", v, GSL_VECTOR_COMPLEX(x, 0)+GSL_VECTOR_COMPLEX(x, 3));  
loopData("loop 1", load1 * GSL_VECTOR_COMPLEX(x, 1), GSL_VECTOR_COMPLEX(x, 1));  
loopData("loop 2", load2 * GSL_VECTOR_COMPLEX(x, 2), GSL_VECTOR_COMPLEX(x, 2));  
loopData("loop 3", load3 * GSL_VECTOR_COMPLEX(x, 3), GSL_VECTOR_COMPLEX(x, 3));  
return 0;  
}