問題八

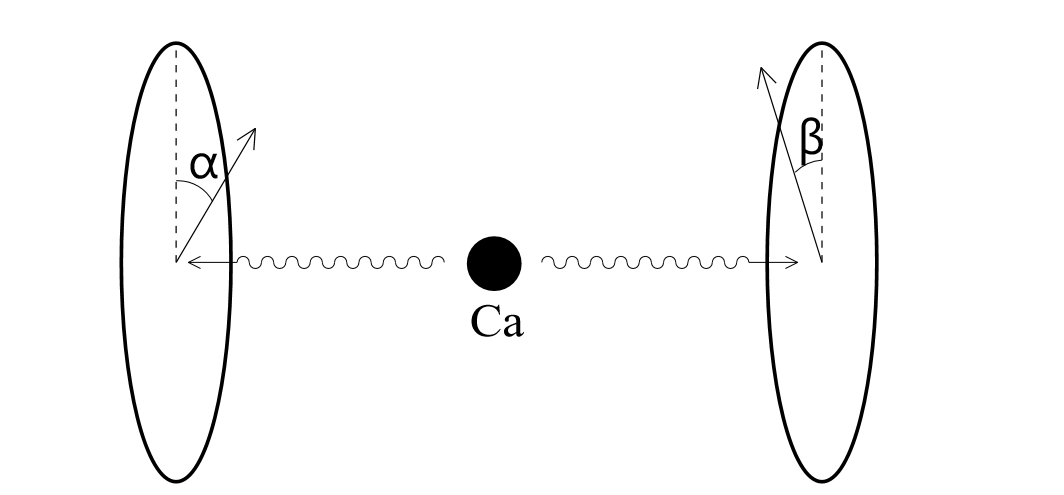
鈣離子發射光子的自旋狀態有兩個 $L_1$ 和 $L_2$ ，假設從左邊看發射源這邊有個量子機率分配 $a = (a_1 , a_2)$ ，從右邊看發射源這邊有個量子機率分配 $(a_2 , a_1)$ ，通過和不通過左邊一個角度 $\alpha$ 的偏振片量子機率 $b(\alpha)$ 的變化是 $x(\alpha) = \begin{bmatrix}\cos(\alpha)&\sin(\alpha)\\-\sin(\alpha)&\cos(\alpha)\end{bmatrix}$ ，類似的，以 $c(\beta)$ 代表通過和不通過右邊一個角度 $\beta$ 的偏振片量子機率，也就是：

$\begin{aligned}b(\alpha) &= (a_1 , a_2) \cdot x(\alpha)\\c(\beta) &= (a_2 , a_1) \cdot x(\beta)\end{aligned}$ （１）如果發射源這邊不管有沒有觀測，都可以在左邊觀測到通過或不通過的機率是1/2和偏光片角度 $\alpha$ 無關，那發射源的量子機率分配是什麼？ $b(\alpha)$ 和 $c(\beta)$ 是什麼？ （２）由 $b(\alpha) = a \cdot x( \alpha )$ 和 $c(\beta) = a \cdot \begin{bmatrix}0&1\\1&0\end{bmatrix} \cdot x(\beta)$ ，求沒有測量發射源的時候，左邊和右邊的通過或不通過機率的關係是什麼？ Ans： （１） 因為 $x$ 是實數，根據問題四的結果，假設 $a = (\sqrt{p} \cdot \exp(i\frac{\pi}{4} ) , \sqrt{1 - p} \cdot \exp(-i\frac{\pi}{4} ) )$ ，而且

$(\frac{1}{2},\frac{1}{2}) = B(\alpha) = ( p \cdot \cos^2(\alpha) + (1 - p) \cdot \sin^2(\alpha), p \cdot \sin^2(\alpha) + (1 - p) \cdot \cos^2(\alpha) )$

所以 $p = \frac{1}{2}$ ，而且：

$\begin{aligned}a &= \left(\frac{1 + i}{2}, \frac{1 - i}{2} \right)\\b(\alpha) &= (a_1 , a_2) \cdot x(\alpha)\\&= \left( \frac{1 + i}{2} \cos(\alpha) - \frac{1 - i}{2} \sin(\alpha) , \frac{1 + i}{2} \sin(\alpha) + \frac{1 - i}{2} \cos(\alpha) \right)\\&= \left( \frac{\exp(i (\alpha + \frac{\pi}{4}) )}{\sqrt{2}},\frac{\exp(i (\alpha - \frac{\pi}{4} )}{\sqrt{2}} \right)\\c(\beta) &= (a_2 ,a_1) \cdot x(\beta)\\&=\left( \frac{1 - i}{2} \cos(\beta) - \frac{1 + i}{2} \sin(\beta) , \frac{1 - i}{2} \sin(\beta) + \frac{1 + i}{2} \cos(\beta) \right)\\&=\left( \frac{\exp( -i (\beta + \frac{\pi}{4}) )}{\sqrt{2}},\frac{\exp( -i (\beta - \frac{\pi}{4}) )}{\sqrt{2}} \right)\end{aligned}$

（2） 因為 $b(\alpha) = a \cdot x( \alpha)$ 和 $c(\beta) = a \cdot \begin{bmatrix}0&1\\1&0\end{bmatrix} \cdot x(\beta)$ ，所以：

$\begin{aligned}c(\beta) &= b(\alpha) \cdot x^{-1}(\alpha) \cdot \begin{bmatrix}0&1\\1&0\end{bmatrix} \cdot x(\beta)\\&= b(\alpha) \cdot \begin{bmatrix}\cos(\alpha)&-\sin(\alpha)\\\sin(\alpha)&\cos(\alpha)\end{bmatrix} \cdot \begin{bmatrix}0&1\\1&0\end{bmatrix} \cdot \begin{bmatrix}\cos(\beta)&\sin(\beta)\\-\sin(\beta)&\cos(\beta)\end{bmatrix}\\&= b(\alpha) \cdot \begin{bmatrix}\sin(\alpha - \beta)&\cos(\alpha - \beta)\\\cos(\alpha - \beta)&-\sin(\alpha - \beta)\end{bmatrix}\end{aligned}$

左邊右邊都有測量，而且 $b(\alpha)$ 又滿足(4)，所以：

$C(\beta) = B(\alpha) \cdot \begin{bmatrix}\sin^2(\alpha - \beta)&\cos^2(\alpha - \beta)\\\cos^2(\alpha - \beta)&\sin^2(\alpha - \beta)\end{bmatrix}$

觀測機率總結是：

$\begin{array}{ccc}\text{left\right}&\text{pass}&\text{not pass}\\\text{pass}& \frac{\sin^2(\alpha - \beta)}{2} & \frac{\cos^2(\alpha - \beta)}{2}\\\text{not pass} & \frac{\cos^2(\alpha - \beta)}{2} & \frac{sin^2(\alpha - \beta)}{2}\end{array}$

藉由變動 $\alpha$，左邊的測量者可以"以無限快的速度影響到機率變數的分布"，這其實只是認知的不同；右邊的測量結果在左邊的測量者得知左邊的測量結果之後在左邊測量者認知中已不再是1/2通過1/2不通過的機率，但是在右邊測量者認知中永遠是1/2通過1/2不通過的機率。

定義

量子糾纏的一般要件其實是：

$z(\alpha , \beta) \equiv x^{-1}(\alpha) \cdot u \cdot y(\beta)， Z_{ij} \equiv z_{ij} \overline{z_{ij}\begin{aligned}b(\alpha) &= a \cdot x (\alpha)\\c(\beta) &= a \cdot u \cdot y(\beta)\\c(\beta) &= b(\alpha) \cdot z(\alpha , \beta)\end{aligned}$

$b(\alpha)$ 和 $z(\alpha , \beta)$ 滿足(4)，但是 $Z$ 卻顯示機率變數沒辦法只是 $\alpha$ 或 $\beta$ 有關的機率變數；操作上來說的意思是， $\alpha_1$ 和 $\beta_1$ 的配置的實驗結果必須和 $\alpha_1$ 和 $\beta_2$ 的配置的實驗結果分開。

對應古典機率的版本：

$\begin{aligned}B(\alpha) &= A \cdot X(\alpha)\\C(\beta) &= A \cdot U \cdot Y(\beta)\end{aligned}$ 機率變數永遠只是 $\alpha$ 或 $\beta$ 有關的機率變數；操作上來說的意思是， $\alpha_1$ 和 $\beta_1$ 的配置的左邊的實驗結果不用和 $\alpha_1$ 和 $\beta_2$ 的配置的左邊的實驗結果分開。

以問題八（A。 Aspect 1962的實驗）而言，應該有八個機率變數，每一列的實驗記錄應該要有8欄，而非4欄。see structure of random variables

如果只有單方面的觀測，則沒有任何統計的方法可以知道對方的 $\alpha$ 或 $\beta$ ，要知道 $\alpha$ 或 $\beta$ 必須同時知道兩方的觀測的結果，例如兩方之間有個蟲洞可以讓實驗者立刻探頭到對方那邊去記錄觀測結果（但是如果兩方之間真的有個蟲洞，那也不用如此大費周章去藉由 quantum entangle 的方式去傳遞資訊，探頭穿過蟲洞去喊一聲就夠了）。在問題八裡，右邊的觀測者沒有任何統計方法可以得到 $\frac{\sin^2(\alpha - \beta)}{2}$ 這個數字，所以無從得知 $\alpha$ 的數值。

所謂傳遞資訊的操作型定義是：影響遠方的對方可以單方面測量的物理現象的機率。量子糾纏無法傳遞資訊，因為左邊的實驗者永遠看到的古典機率分布是 $B(\alpha)$ ，不同的 $\beta$ 無法影響，右邊的實驗者永遠看到的古典機率分布是 $C(\beta)$ ，不同的 $\alpha$ 無法影響。如果資訊能無限快傳遞，配上3D列印技術，物體就可以無限快移動。