直流電路的最終電壓電流

HomePage | Memberswill go by tor | RecentChanges | Join |

See 數學線性微分方程知識 for formula reference.

例題一

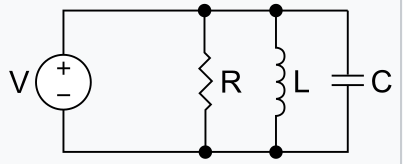
求這個直流電路的電壓和電流。

有三個迴路，分別給一個電阻器，一個電感器，和一個電容器：

0=[I 1t dI 2tdt Q t][−R 0 0 0 −L 0 0 0 −1C]+[V V V]0 = \begin{bmatrix}I_{1 t}&\frac{d I_{2t}}{d t}&Q_t\end{bmatrix} \begin{bmatrix}-R&0&0\\0&-L&0\\0&0&-\frac{1}{C}\end{bmatrix} + \begin{bmatrix}V&V&V\end{bmatrix}

所以

I 1t=VR Q t=CV dI 2tdt=VL\begin{aligned}I_{1 t} = \frac{V}{R}\\Q_t = C V\\\frac{d I_{2 t}}{d t} = \frac{V}{L}\end{aligned}

對照 dx tdt=x tA+B,A=0,B=VL\frac{d x_t}{d t} = x_t A + B,A = 0,B = \frac{V}{L} ，所以 I 2t=VLt+I 20I_{2 t} = \frac{V}{L} t + I_{20}

例題二

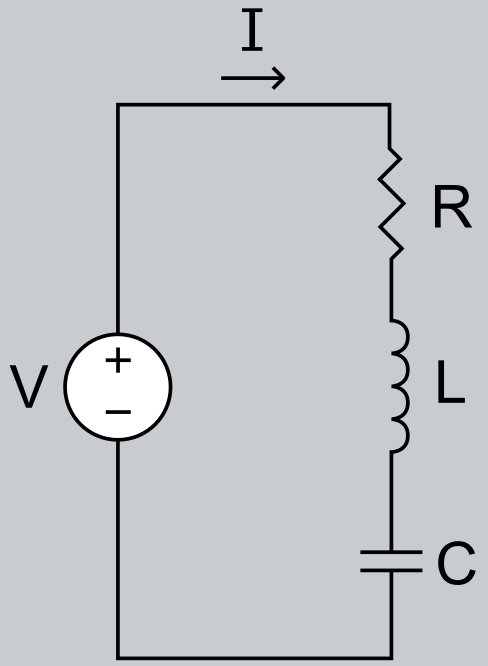
求這個直流電路的最終的電壓和電流。

0=[dI tdt I t Q t dQ tdt][−L 0 −R 1 −1C 0 0 −1]+[V 0]=[dI tdt dQ tdt][−L 0 0 −1]+[I t Q t][−R 1 −1C 0]+[V 0]0 = \begin{bmatrix}\frac{d I_t}{d t}&I_t&Q_t&\frac{d Q_t}{d t}\end{bmatrix} \begin{bmatrix}-L&0\\-R&1\\-\frac{1}{C}&0\\0&-1\end{bmatrix} + \begin{bmatrix}V&0\end{bmatrix}= \begin{bmatrix}\frac{d I_t}{d t}&\frac{d Q_t}{d t}\end{bmatrix} \begin{bmatrix}-L&0\\0&-1\end{bmatrix} + \begin{bmatrix}I_t&Q_t\end{bmatrix} \begin{bmatrix}-R&1\\-\frac{1}{C}&0\end{bmatrix} + \begin{bmatrix}V&0\end{bmatrix}

所以

[dI tdt dQ tdt]=[I t Q t][−RL 1 −1LC 0]+[VL 0]\begin{bmatrix}\frac{d I_t}{d t}&\frac{d Q_t}{d t}\end{bmatrix} = \begin{bmatrix}I_t&Q_t\end{bmatrix} \begin{bmatrix}-\frac{R}{L}&1\\-\frac{1}{L C}&0\end{bmatrix} + \begin{bmatrix}\frac{V}{L}&0\end{bmatrix}

對照 dx tdt=x tA+B\frac{d x_t}{d t} = x_t A + B ，

A=[−RL 1 −1LC 0] B=[VL 0]\begin{aligned}A = \begin{bmatrix}-\frac{R}{L}&1\\-\frac{1}{L C}&0\end{bmatrix}\\B=\begin{bmatrix}\frac{V}{L}&0\end{bmatrix}\end{aligned}

所以最終狀態是

−[VL 0][−RL 1 −1LC 0] −1=[0 CV]-\begin{bmatrix}\frac{V}{L}&0\end{bmatrix} \begin{bmatrix}-\frac{R}{L}&1\\-\frac{1}{L C}&0\end{bmatrix}^{-1}= \begin{bmatrix}0&C V\end{bmatrix} 直流電路裡面的電容器和電感器都是很無聊的。如果有最終電壓電流，電容器的電壓和電感器的電流都不會變，整個電路實際上只是變成直流電壓源和電阻的電路。但是如果配上一些開關管 MOSFET，電路就變成片段式的微分方程，電容器和電感器就可以真的有用處，因為每個片段的開頭和結尾的電壓電流的不同，即使相差只是一點點，但是除以時間差之後的導數值還是不可忽略。

例題三

一個直流電變壓器 ( DC-DC converter )。把輸入的電壓換成另一個數值的電壓：

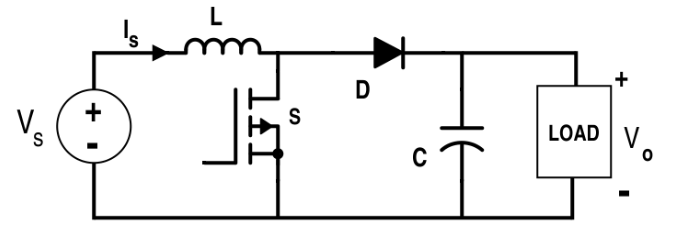
當開關管是 ON 的時候，電路是

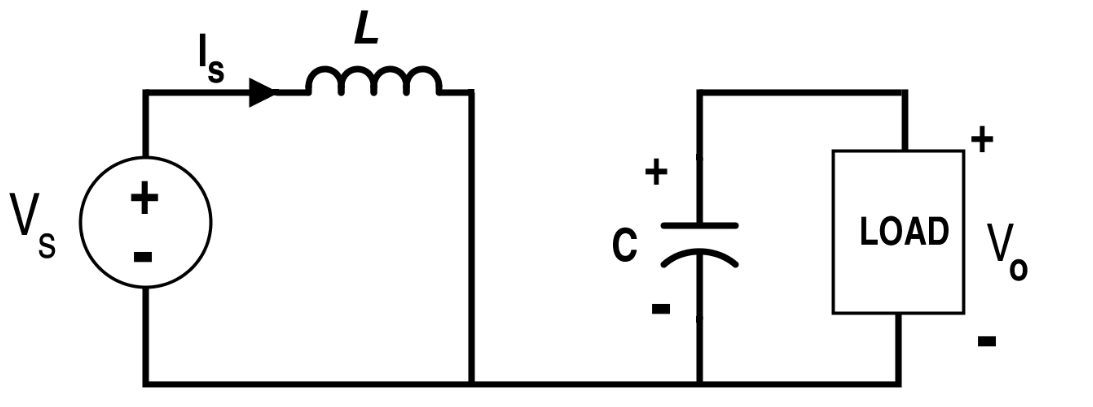
當開關管是 OFF 的時候，電路是

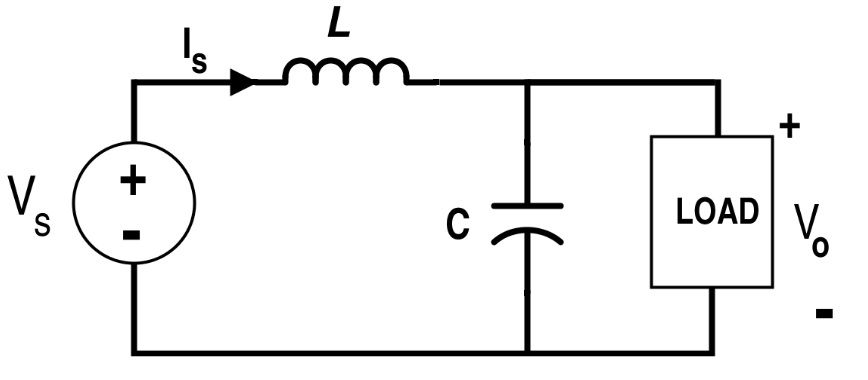
LOAD 是一個電阻。求最終狀態。

ON 的時候的微分方程式是：

0=V−LdI sdt 0=V c−RI o I o=−dV cdt\begin{aligned}0 = V - L \frac{d I_s}{d t}\\0 = V_c - R I_o\\I_o = - \frac{d V_c}{d t}\end{aligned}

OFF 的時候的微分方程式是：

0=V−LdI sdt−V c 0=V c−RI o I o−Is=−dV cdt\begin{aligned}0 = V - L \frac{d I_s}{d t} - V_c\\0 = V_c - R I_o\\I_o - I s = - \frac{d V_c}{d t}\end{aligned}

把 I oI_o 用 V cR\frac{V_c}{R} 代換掉，並寫成矩陣。

在開關管 ON 的時候：

0=[dI sdt dV cdt][−L 0 0 1]+[I s V c][0 0 0 1R]+[V 0] [dI sdt dV cdt]=[I s V c][0 0 0 −1R]+[VL 0]\begin{aligned}0 = \begin{bmatrix}\frac{d I_s}{d t}&\frac{d V_c}{d t}\end{bmatrix} \begin{bmatrix}-L&0\\0&1\end{bmatrix} + \begin{bmatrix}I_s&V_c\end{bmatrix} \begin{bmatrix}0&0\\0&\frac{1}{R}\end{bmatrix} + \begin{bmatrix}V&0\end{bmatrix}\\\begin{bmatrix}\frac{d I_s}{d t}&\frac{d V_c}{d t}\end{bmatrix} = \begin{bmatrix}I_s&V_c\end{bmatrix} \begin{bmatrix}0&0\\0&-\frac{1}{R}\end{bmatrix} + \begin{bmatrix}\frac{V}{L}&0\end{bmatrix}\end{aligned}

在開關管 OFF 的時候：

0=[dI sdt dV cdt][−L 0 0 1]+[I s V c][0 −1 −1 1R]+[V 0] [dI sdt dV cdt]=[I s V c][0 1 −1L −1R]+[VL 0]\begin{aligned}0 = \begin{bmatrix}\frac{d I_s}{d t}&\frac{d V_c}{d t}\end{bmatrix} \begin{bmatrix}-L&0\\0&1\end{bmatrix} + \begin{bmatrix}I_s&V_c\end{bmatrix} \begin{bmatrix}0&-1\\-1&\frac{1}{R}\end{bmatrix} + \begin{bmatrix}V&0\end{bmatrix}\\\begin{bmatrix}\frac{d I_s}{d t}&\frac{d V_c}{d t}\end{bmatrix} = \begin{bmatrix}I_s&V_c\end{bmatrix} \begin{bmatrix}0&1\\-\frac{1}{L}&-\frac{1}{R}\end{bmatrix} + \begin{bmatrix}\frac{V}{L}&0\end{bmatrix}\end{aligned}

這是片段式的線性常微分方程，以 dd 表示開關管 ON 的時間的比例，開關管 ON OFF 一個周期的時間很短，則

A=d[0 0 0 −1R]+(1−d)[0 1 −1L −1R]=[0 1−d −1−dL −1R] B=d[VL 0]+(1−d)[VL 0]=[VL 0]\begin{aligned}A = d \begin{bmatrix}0&0\\0&-\frac{1}{R}\end{bmatrix} + (1 - d) \begin{bmatrix}0&1\\-\frac{1}{L}&-\frac{1}{R}\end{bmatrix} = \begin{bmatrix}0&1 - d\\-\frac{1 - d}{L}&-\frac{1}{R}\end{bmatrix}\\B = d \begin{bmatrix}\frac{V}{L}&0\end{bmatrix} + (1 - d) \begin{bmatrix}\frac{V}{L}&0\end{bmatrix}= \begin{bmatrix}\frac{V}{L}&0\end{bmatrix}\end{aligned}

最後的穩定狀態是

[I s V c]=−BA −1=[VR(1−d) 2 V1−d]\begin{bmatrix}I_s&V_c\end{bmatrix} = - B A^{-1} = \begin{bmatrix}\frac{V}{R ( 1 - d )^2}&\frac{V}{1 - d}\end{bmatrix}

輸出直流電壓對輸入直流電壓的比值是 11−d\frac{1}{1 - d}

電池

一個電池的電流和電壓的關係稱之為 IV curve。電流畫在橫軸，正電流代表放電，電壓畫在縱軸，橫軸截距稱之為 short-circuit current，也就是發生短路時候的電流，縱軸截距稱之為 open-circuit voltage，也就是沒有在充放電的時候測量的電壓 。不同的電池的IV curve 樣子不同，但是都是電流越大電壓越低。除了太陽電池的 short-circuit current 不大以外，一般的電池的 short-circuit current 通常很大到可能引發火災的地步。IV curve 在一個小區域可以視為一個負斜率的直線，這個斜率大小也是電池內部電阻。 V 直流電壓充電的時候，0=V−bat−Ir0=V-bat-I r，三用電表量到的是 bat+Irbat+I r。電池放電的時候，0=bat−Ir−IR0=bat-I r - I R ，三用電表量到的是 bat−Irbat-I r。所以 batbat 也是 open-circuit voltage，充電的時候電池的電壓偏高，放電的時候電池的電壓偏低；不像汽油表尺，表尺多高就是精確的表示有多少油，尤其是快充電流很大，充電的時候看到電壓偏高就以為電充夠了就急忙上路搞不好半路車沒電。rr 和 batbat 有關，電池電量越滿或越餓的時候 rr 比較大，但是和 II 無關；如果一個電池的容量很大，則 batbat 幾乎不變。最基礎的電池叫做 cell，利用某種化學或物理反應產生電壓。cell 可以很大有很大的容量，但是電壓還是和一個小容量的 cell 一樣。太陽能光電池無法蓄電，只能在照到光的時候放電，每個 cell 的 open-circuit voltage 約在 0.5 伏特。鉛酸電池可以充放電，每個 cell 的 open-circuit voltage 約在 2.1 伏特。鋰鐵電池可以充放電，每個 cell 的 open-circuit voltage 約在 3.2 伏特。鋰電池可以充放電，每個 cell 的 open-circuit voltage 約在 3.8 伏特。電池 cell 總是可以藉由串聯來增加電壓和藉由並聯來增加容量。一個等效的代表總和的電池，串聯時候內電阻增加 (IV curve 縱軸方向相加)，並聯時候內電阻減少 (IV curve 橫軸方向相加)。一個便利商店賣的 1.5 伏特乾電池就是一個 cell。一塊 12 伏特系統用的太陽板有 36 個 cell，方便去充電一個 12 伏特的電池。一個車用鉛酸啟動電池其實是 6 個鉛酸電池 cell 串聯得到 12 伏特的電壓。一個車用鋰鐵啟動電池其實是 4 個鋰鐵電池 cell 串聯得到 12 伏特電壓。一個電動車的鋰電池的電壓是 400 伏特，是很多鋰電池 cell 的串聯。很多時候業主一個 cell 壞掉就整個電池換掉，所以常有還算正常的二手鋰鐵電池或鋰電池 cell 在市場上賣。

一個直流電源的輸出直流電壓 VV，輸出電流 I 0I_0 ，並聯一個電池和一個代表負載的電阻 RR，電池的 open-circuit voltage 是 batbat，內電阻是 rr，電池迴路的電流是 I 1I_1 ，負載迴路的電流是 I 2I_2 ，所以：

I 0=I 1+I 2 V=bat+I 1r V=I 2R\begin{aligned}I_0 = I_1 + I_2\\V = bat + I_1 r\\V = I_2 R\end{aligned}

所以 I 1=I 01+rR−batR+rI_1 = \frac{I_0}{1 + \frac{r}{R}} - \frac{bat}{R + r} ，也就是 V=bat1+rR+I 0r1+rRV = \frac{bat}{1 + \frac{r}{R}} + I_0 \frac{r}{1 + \frac{r}{R}} ，數學上等效於直接單獨充電一個假想電池，open-circuit voltage 是 bat1+rR\frac{bat}{1 + \frac{r} {R}} ，內電阻是 r1+rR\frac{r}{1 + \frac{r}{R}} 。給定 batbat 和電池內電阻 rr 和代表負載的 RR， V=bat1+rR+I 0r1+rRV = \frac{bat}{1 + \frac{r}{R}} + I_0 \frac{r}{1 + \frac{r}{R}} 這個直線限定了VV 和 I 0I_0 的關係。 VI 0V I_0 這個瓦數提供充電和一個直流負載。電池內電阻發的熱不算，充電用掉的瓦數是 W bat=batI 1W_{bat} = bat I_1 ，直流負載用掉的瓦數是 W R=VI 2W_R = V I_2 。如果 I 1<0I_1&lt; 0 則表示是電池放電來協助提供負載瓦數。充電瓦數的比例是

W batVI 0=bat(I 01+rR−batR+r)VI 0=bat(I 0R−bat)VI 0(R+r)\frac{W_{bat}}{V I_0} = \frac{bat \left( \frac{I_0}{1 + \frac{r}{R}} - \frac{bat}{R + r} \right)}{V I_0} = \frac{bat ( I_0 R - bat )}{V I_0 ( R + r )}

如果 I 0<batRI_0 &lt; \frac{bat}{R} ，則電池沒有充電而是在放電。如果負載電阻很大，則充電瓦數比例是 batV\frac{bat}{V} 。

例題四

一個直流電變壓器 ( DC-DC converter )。把輸入的電壓換成另一個數值的電壓：

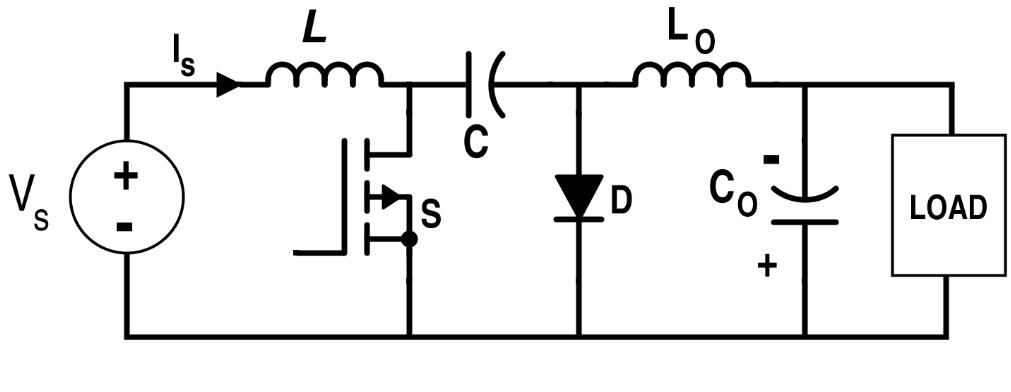
當開關管是 ON 的時候，電路是

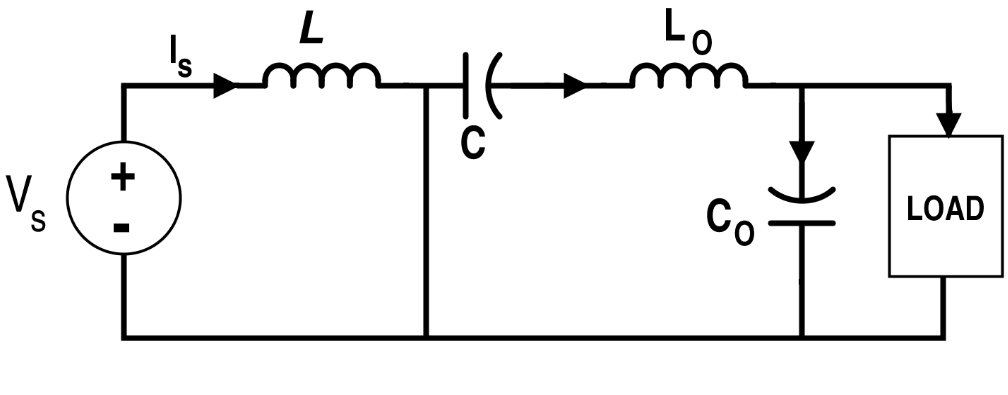
當開關管是 OFF 的時候，電路是

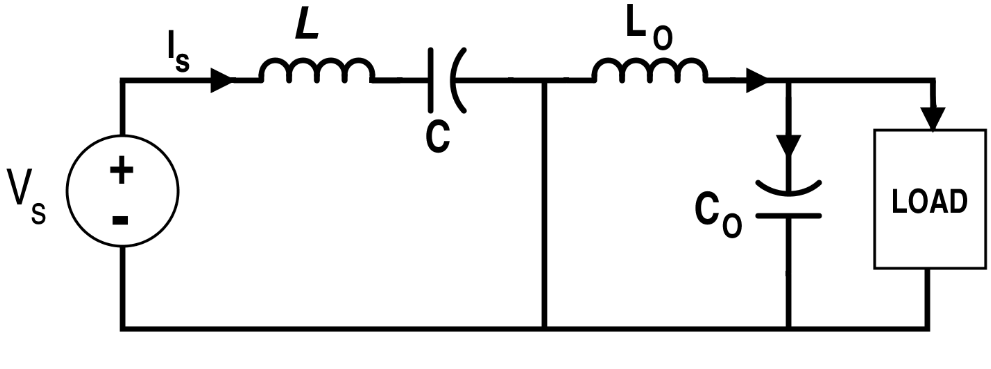
LOAD 是一個被充電的電池，open-circuit voltage 是 batbat，內電阻是 RR。求最終狀態。

ON 的時候的微分方程式是：

0=V−LdI sdt 0=−V c−L odI cdt+V o 0=−V o+bat−RI o I c−I o=−C odV odt I c=CdV cdt\begin{aligned}0 = V - L \frac{d I_s}{d t}\\0 = - V_c - L_o \frac{d I_c}{d t} + V_o\\0 = - V_o + bat - R I_o\\I_c - I_o = - C_o \frac{d V_o}{d t}\\I_c = C \frac{d V_c}{d t}\end{aligned}

OFF 的時候的微分方程式是：

0=V−LdI sdt−V c 0=−L odI cdt+V o 0=−V o+bat−RI o I s=CdV cdt I c−I o=−C odV odt\begin{aligned}0 = V - L \frac{d I_s}{d t} - V_c\\0 = - L_o \frac{d I_c}{d t} + V_o\\0 = - V_o + bat - R I_o\\I_s = C \frac{d V_c}{d t}\\I_c - I_o = - C_o \frac{d V_o}{d t}\end{aligned}

把 I oI_o 用 −V o+batR\frac{-V_o + bat}{R} 代換掉。ON 的時候：

0=V−LdI sdt 0=−V c−L odI cdt+V o 0=I c+V o−batR+C odV odt 0=−I c+CdV cdt\begin{aligned}0 = V - L \frac{d I_s}{d t}\\0 = - V_c - L_o \frac{d I_c}{d t} + V_o\\0 = I_c + \frac{V_o - bat}{R} + C_o \frac{d V_o}{d t}\\0 = - I_c + C \frac{d V_c}{d t}\end{aligned}

OFF 的時候：

0=V−LdI sdt−V c 0=−L odI cdt+V o 0=−I s+CdV cdt 0=I c+V o−batR+C odV odt\begin{aligned}0 = V - L \frac{d I_s}{d t} - V_c\\0 = - L_o \frac{d I_c}{d t} + V_o\\0 = - I_s + C \frac{d V_c}{d t}\\0 = I_c + \frac{V_o - bat}{R} + C_o \frac{d V_o}{d t}\end{aligned}

寫成矩陣。ON 的時候：

0=[dI sdt dI cdt dV cdt dV odt][−L 0 0 0 0 −L o 0 0 0 0 0 C 0 0 C o 0]+[I s I c V c V o][0 0 0 0 0 0 1 −1 0 −1 0 0 0 1 1R 0]+[V 0 −batR 0]0 = \begin{bmatrix}\frac{d I_s}{d t}&amp;\frac{d I_c}{d t}&amp;\frac{d V_c}{d t}&amp;\frac{d V_o}{d t}\end{bmatrix} \begin{bmatrix}-L&amp;0&amp;0&amp;0\\0&amp;-L_o&amp;0&amp;0\\0&amp;0&amp;0&amp;C\\0&amp;0&amp;C_o&amp;0\end{bmatrix} + \begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} \begin{bmatrix}0&amp;0&amp;0&amp;0\\0&amp;0&amp;1&amp;-1\\0&amp;-1&amp;0&amp;0\\0&amp;1&amp;\frac{1}{R}&amp;0\end{bmatrix} + \begin{bmatrix}V&amp;0&amp;-\frac{bat}{R}&amp;0\end{bmatrix}

也就是

[dI sdt dI cdt dV cdt dV odt]=[I s I c V c V o][0 0 0 0 0 0 1C −1C o 0 −1L o 0 0 0 1L o 0 −1RC o]+[VL 0 0 batRC o]\begin{bmatrix}\frac{d I_s}{d t}&amp;\frac{d I_c}{d t}&amp;\frac{d V_c}{d t}&amp;\frac{d V_o}{d t}\end{bmatrix}=\begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} \begin{bmatrix}0&amp;0&amp;0&amp;0\\0&amp;0&amp;\frac{1}{C}&amp;-\frac{1}{C_o}\\0&amp;-\frac{1}{L_o}&amp;0&amp;0\\0&amp;\frac{1}{L_o}&amp;0&amp;-\frac{1}{R C_o}\end{bmatrix}+\begin{bmatrix}\frac{V}{L}&amp;0&amp;0&amp;\frac{bat}{R C_o}\end{bmatrix}

OFF 的時候：

0=[dI sdt dI cdt dV cdt dV odt][−L 0 0 0 0 −L o 0 0 0 0 C 0 0 0 0 C o]+[I s I c V c V o][0 0 −1 0 0 0 0 1 −1 0 0 0 0 1 0 1R]+[V 0 0 −batR]0 = \begin{bmatrix}\frac{d I_s}{d t}&amp;\frac{d I_c}{d t}&amp;\frac{d V_c}{d t}&amp;\frac{d V_o}{d t}\end{bmatrix} \begin{bmatrix}-L&amp;0&amp;0&amp;0\\0&amp;-L_o&amp;0&amp;0\\0&amp;0&amp;C&amp;0\\0&amp;0&amp;0&amp;C_o\end{bmatrix} + \begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} \begin{bmatrix}0&amp;0&amp;-1&amp;0\\0&amp;0&amp;0&amp;1\\-1&amp;0&amp;0&amp;0\\0&amp;1&amp;0&amp;\frac{1}{R}\end{bmatrix} + \begin{bmatrix}V&amp;0&amp;0&amp;-\frac{bat}{R}\end{bmatrix}

也就是

[dI sdt dI cdt dV cdt dV odt]=[I s I c V c V o][0 0 1C 0 0 0 0 −1C o −1L 0 0 0 0 1L o 0 −1RC o]+[VL 0 0 batRC o]\begin{bmatrix}\frac{d I_s}{d t}&amp;\frac{d I_c}{d t}&amp;\frac{d V_c}{d t}&amp;\frac{d V_o}{d t}\end{bmatrix} = \begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} \begin{bmatrix}0&amp;0&amp;\frac{1}{C}&amp;0\\0&amp;0&amp;0&amp;-\frac{1}{C_o}\\-\frac{1}{L}&amp;0&amp;0&amp;0\\0&amp;\frac{1}{L_o}&amp;0&amp;-\frac{1}{R C_o}\end{bmatrix} + \begin{bmatrix}\frac{V}{L}&amp;0&amp;0&amp;\frac{bat}{R C_o}\end{bmatrix}

這是片段式的線性微分方程，以 dd 表示開關管 ON 的時間的比例，則

A=d[0 0 0 0 0 0 1C −1C o 0 −1L o 0 0 0 1L o 0 −1RC o]+(1−d)[0 0 1C 0 0 0 0 −1C o −1L 0 0 0 0 1L o 0 −1RC o]=[0 0 1−dC 0 0 0 dC −1C o −1−dL −dL o 0 0 0 1L o 0 −1RC o] B=d[VL 0 0 batRC o]+(1−d)[VL 0 0 batRC o]=[VL 0 0 batRC o]\begin{aligned}A = d \begin{bmatrix}0&amp;0&amp;0&amp;0\\0&amp;0&amp;\frac{1}{C}&amp;-\frac{1}{C_o}\\0&amp;-\frac{1}{L_o}&amp;0&amp;0\\0&amp;\frac{1}{L_o}&amp;0&amp;-\frac{1}{R C_o}\end{bmatrix} +(1-d) \begin{bmatrix}0&amp;0&amp;\frac{1}{C}&amp;0\\0&amp;0&amp;0&amp;-\frac{1}{C_o}\\-\frac{1}{L}&amp;0&amp;0&amp;0\\0&amp;\frac{1}{L_o}&amp;0&amp;-\frac{1}{R C_o}\end{bmatrix}=\begin{bmatrix}0&amp;0&amp;\frac{1-d}{C}&amp;0\\0&amp;0&amp;\frac{d}{C}&amp;-\frac{1}{C_o}\\-\frac{1-d}{L}&amp;-\frac{d}{L_o}&amp;0&amp;0\\0&amp;\frac{1}{L_o}&amp;0&amp;-\frac{1}{R C_o}\end{bmatrix}\\B = d \begin{bmatrix}\frac{V}{L}&amp;0&amp;0&amp;\frac{bat}{R C_o}\end{bmatrix} + (1 - d) \begin{bmatrix}\frac{V}{L}&amp;0&amp;0&amp;\frac{bat}{R C_o}\end{bmatrix} = \begin{bmatrix}\frac{V}{L}&amp;0&amp;0&amp;\frac{bat}{R C_o}\end{bmatrix}\end{aligned}

最後的穩定狀態是：

[I s I c V c V o]=−BA −1=[d 2V(1−d) 2−bat⋅d1−dR bat−dV1−dR V1−d dV1−d]\begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} = - B A^{-1} = \begin{bmatrix}\frac{\frac{d^2 V}{(1 - d)^2} - \frac{bat \cdot d}{1 - d}}{R}&amp;\frac{bat- \frac{d V}{1 - d}}{R}&amp;\frac{V}{1 - d}&amp;\frac{d V}{1 - d}\end{bmatrix}

因為是充電，所以 V o=dV1−d>batV_o = \frac{d V}{1 - d}&gt; bat ，這個直流電變壓器的輸出直流電壓對輸入直流電壓的比值是 d1−d\frac{d}{1 - d} 。如果電容器的電壓解出來是負的，代表電容器正電位的腳畫錯。習慣上電流在一個迴路裡面順時鐘方向，如果電流解出來是負的，代表電流的方向和原本畫的相反。這在數學上並沒有問題。

展到 T 的一次方 (藉由 Mathematica™ 幫忙數學運算)。

[I s I c V c V o] =−(∑ k=1 Kd kB kβ(Td kA k)∏ j=k+1 Kα(Td jA j))(1T(∏ j=1 Kα(Td jA j)−I)) −1 x 0 =[d 2V(1−d) 2−bat⋅d1−dR bat−dV1−dR V1−d dV1−d]+T[−dV2L 0 0 0] x 1 =[d 2V(1−d) 2−bat⋅d1−dR bat−dV1−dR V1−d dV1−d]+T[dV2L −dVL o bat⋅d−d 2V1−dRC 0]\begin{aligned}\begin{bmatrix}I_s&amp;I_c&amp;V_c&amp;V_o\end{bmatrix} &amp;= -\left(\sum_{k = 1}^K {d_k B_k \beta(T d_k A_k) \prod_{j = k + 1}^K \alpha(T d_j A_j)} \right) \left(\frac{1}{T} \left(\prod_{j = 1}^K \alpha(T d_j A_j) - I\right)\right)^{-1}\\x_0 &amp;= \begin{bmatrix}\frac{\frac{d^2 V}{(1 - d)^2} - \frac{bat \cdot d}{1 - d}}{R}&amp;\frac{bat- \frac{d V}{1 - d}}{R}&amp;\frac{V}{1 - d}&amp;\frac{d V}{1 - d}\end{bmatrix} + T \begin{bmatrix}-\frac{d V}{2 L}&amp;0&amp;0&amp;0\end{bmatrix}\\x_1 &amp;= \begin{bmatrix}\frac{\frac{d^2 V}{(1 - d)^2} - \frac{bat \cdot d}{1 - d}}{R}&amp;\frac{bat- \frac{d V}{1 - d}}{R}&amp;\frac{V}{1 - d}&amp;\frac{d V}{1 - d}\end{bmatrix} + T \begin{bmatrix}\frac{d V}{2 L}&amp;-\frac{d V}{L_o}&amp;\frac{bat \cdot d - \frac{d^2 V}{1 - d}}{R C}&amp;0\end{bmatrix}\end{aligned}

最終狀態在兩個狀態間鋸齒狀擺盪，縮短週期 TT 或是加大電感值和電容值可以把這個鋸齒變小。一般 TT 很短，界於 1/200k 到 1/100k 秒之間。

逆變器對應的等效電阻

(參見 交流電路的最終電壓電流)因為交流電的功率等於 12v 2kcos(θ)\frac{1}{2} v^2 k \cos(\theta) ，其中 kk 和 cos(θ)\cos(\theta) 根據接上的機器規格而定， vv 是交流電壓的最大值， vkv k 是交流電流的最大值， θ\theta 是電流和電壓相差的角度。以 II 表示輸入電流。以 gg 表示逆變器的直流輸入電壓和交流輸出電壓的大小的比例；例如一個把直流電 24 伏特換成交流電 240 伏特的逆變器 g=10g = 10 。因為輸入瓦數等於輸出瓦數，假設逆變器效率 100%，則 VI=12(Vg2) 2kcos(θ)=V 2g 2kcos(θ)V I = \frac{1}{2} (V g \sqrt{2})^2 k \cos(\theta) = V^2 g^2 k \cos(\theta) ，也就是 I = V g 2 k c o s ⁡ \theta ，等效電阻是 R=VI=1g 2kcos(θ)R = \frac{V}{I} = \frac{1}{g^2 k \cos(\theta)} 。如果逆變器沒接上負載或是逆變器接上一個交流電壓變壓器但是變壓器沒接上負載，這時候的等效電阻 RR 等於無限大。

假設逆變器效率 hh，則 R=hg 2kcos(θ)R = \frac{h}{g^2 k \cos(\theta)}

充電控制器

太陽電池上的電壓 V sV_s 和電流 I sI_s   必須在當下日照的太陽電池的 IV curve 上。連接太陽電池的充電控制器內建有一個直流電變壓器，會調整開關管的 dd 數值，讓太陽電池上的電壓 V sV_s 和輸出的直流電壓 V oV_o 之間的比例對應的輸出瓦數 V oI 0V_o I_0 最大。以 hh 代表充電控制器的效率，數學上來說是這樣：先在太陽電池的 IV curve 上找出最大瓦數的點 (I s,V s)(I_s,V_s) ，然後畫出這個最大瓦數的電流電壓的曲線 IV=I sV shI V = I_s V_s h ，然後和直線 V=bat1+rR+Ir1+rRV = \frac{bat}{1 + \frac{r}{R}} + I \frac{r}{1 + \frac{r}{R}} 的交叉點就是充電控制器輸出的電流和電壓 (I 0,V o)(I_0,V_o) ，接著由 V oV s\frac{V_o}{V_s} 這個比值決定出最好的 dd。但是工程上很難事先知道 rr 和 RR，所以做法是不停得試不同的 dd，看 V oI 0V_o I_0 值是不是最大。但是 "不停的試去找 dd" 背後的假設是日照沒變和負載沒變，而實際情況是這兩個經常一直在變，所以有時候充電控制器裡面控制晶片的演算法不夠聰明就會讓輸出電壓不是最佳功率。充電控制器的輸出電壓 VV 是被動決定的，相對於訂好的電壓範圍可能會太高或太低，這時候充電控制器裡面的控制晶片就把電路斷開避免造成下游機器的損傷。充電控制器斷開並不會有太大影響，這等同於晚上沒日照，輸出迴路上的負載還是能藉由輸出迴路上並聯的電池的放電得到功率。